Базисы на плоскости и в пространстве

Рис. 5.2

Базисом на плоскости называется любая упорядоченная пара

линейно независимых (неколлинеарных) векторов. Поскольку три вектора на плоскости линейно зависимы, то любой вектор на плоскости можно единственным образом разложить по базису – представить в виде линейной комбинации базисных векторов:

,

где числа 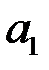, – координаты вектора в выбранном базисе (рис. 5.2).

Записи и означают, что вектор имеет в выбранном базисе координаты , .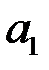

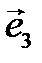
Рис. 5.3.

Базисом в пространстве называется любая упорядоченная тройка линейно независимых (некомпланарных) векторов. Поскольку четыре вектора в пространстве линейно зависимы, то любой вектор в пространстве можно разложить по базису – представить в виде линейной комбинации базисных векторов (рис. 5.3):

, .

Числа определяются по вектору однозначно; они называются координатами вектора в выбранном базисе. Используется также запись или .

Таким образом, при фиксированном базисе на плоскости (в пространстве) каждый вектор однозначно описывается упорядоченным набором из двух (трех чисел). Все действия с векторами: линейные операции, а также действия, которые будут определены в дальнейшем, выражаются через координаты векторов, то есть сводятся к числовым вычислениям. В этом и состоит смысл введения координат.

Линейные операции в координатах. Если в некотором базисе в пространстве , , то в том же базисе

, , (5.2)

то есть при сложении векторов соответствующие координаты складываются, при умножении вектора на число λ каждая координата вектора умножается на это число.

Аналогичное правило, конечно, верно и для векторов на плоскости.

Критерий коллинеарности: Два ненулевых вектора и коллинеарны (линейно зависимы) тогда и только тогда, когда они и их координаты пропорциональны:

. (5.3)

Критерий компланарности: Три вектора , и компланарны (линейно зависимы) тогда и только тогда, когда определитель

. (5.4)

Ортонормированным базисом называется базис из взаимно перпендикулярных векторов единичной длины. Фиксированный ортонормированный базис на плоскости будем обозначать , в пространстве – .