 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Базисы в линейном пространстве
|
|
Упорядоченный набор векторов
 (5.5)
(5.5)
линейного пространства  образуют базис в
образуют базис в  , если
, если
1) векторы (5.5) линейно независимы,
2) любой вектор  можно представить в виде линейной комбинации векторов (5.5):
можно представить в виде линейной комбинации векторов (5.5):
 . (5.6)
. (5.6)
Равенство (5.6) называется разложением вектора  по базису (5.5). Для каждого вектора
по базису (5.5). Для каждого вектора  числа
числа  определяются однозначно; они называются координатами вектора
определяются однозначно; они называются координатами вектора  в базисе (5.5).
в базисе (5.5).
При фиксированном базисе соответствие между векторами 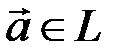 и их координатными строками – арифметическими векторами
и их координатными строками – арифметическими векторами  взаимно-однозначно: каждому вектору соответствует единственная строка, разным векторам – разные строки. Как и в случае геометрических векторов, при сложении двух векторов их координатные строки складываются, при умножении на число – умножаются на это число. Вышесказанное позволяет при выполнении линейных операций фактически отождествить вектор
взаимно-однозначно: каждому вектору соответствует единственная строка, разным векторам – разные строки. Как и в случае геометрических векторов, при сложении двух векторов их координатные строки складываются, при умножении на число – умножаются на это число. Вышесказанное позволяет при выполнении линейных операций фактически отождествить вектор  с его координатной строкой и писать
с его координатной строкой и писать  .
.
Линейные пространства, в которых существует базис, называются конечномерными. Можно показать, что любой базис в конечномерном линейном пространстве  содержит одно и то же число векторов. Это число
содержит одно и то же число векторов. Это число  называется размерностью линейного пространства
называется размерностью линейного пространства  ; говорят, что
; говорят, что  –
–  - мерное линейное пространство и обозначают его с указанием размерности:
- мерное линейное пространство и обозначают его с указанием размерности:  .
.
Согласно п. 5.1.5 линейное пространство  геометрических векторов на плоскости двумерно, линейное пространство
геометрических векторов на плоскости двумерно, линейное пространство  геометрических векторов в пространстве трехмерно. Пространство
геометрических векторов в пространстве трехмерно. Пространство 
 -мерно.
-мерно.
Линейное пространство, в котором существует любое число линейно независимых векторов и потому не существует базиса, называется бесконечномерным. Например, бесконечномерным является линейное пространство  всех функций на
всех функций на  (см. задачу 5.3.20).
(см. задачу 5.3.20).
Дата публикования: 2015-09-17; Прочитано: 301 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
