 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные операции над векторами
|
|
Пусть  и
и 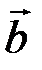 – векторы на плоскости (в пространстве).
– векторы на плоскости (в пространстве).
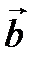
|
| A |
| B |
| C |
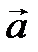
|
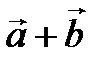
|
| D |
| Рис. 5.1 |
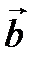
|
 и
и 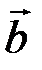 называется вектор
называется вектор 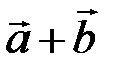 , определяемый по «правилу треугольника»: строим
, определяемый по «правилу треугольника»: строим 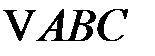 так, чтобы
так, чтобы 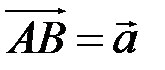 ,
, 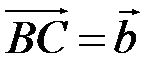 , тогда
, тогда 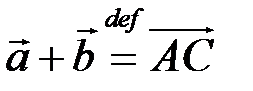 (рис.5.1).
(рис.5.1).
Если векторы не параллельны, то их сумму можно найти по «правилу параллелограмма»: строим параллелограмм 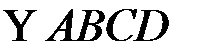 так, чтобы
так, чтобы 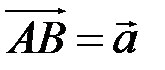 ,
, 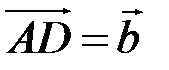 , тогда
, тогда 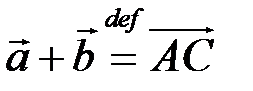 – диагональ параллелограмма (рис. 5.1). Это правило удобно для нахождения суммы векторов сил, приложенных в одной точке – равнодействующей силы.
– диагональ параллелограмма (рис. 5.1). Это правило удобно для нахождения суммы векторов сил, приложенных в одной точке – равнодействующей силы.
Произведение вектора  на число
на число 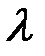 (
(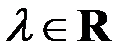 ) называется вектор
) называется вектор 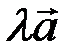 , длина которого равна произведению
, длина которого равна произведению 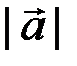 на
на 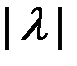 , а направление то же, что и у вектора
, а направление то же, что и у вектора  при
при 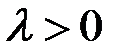 и противоположное при
и противоположное при 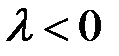 (при
(при 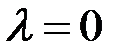 получается нулевой вектор:
получается нулевой вектор: 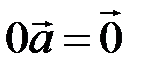 ).
).
Операции сложения векторов и умножения вектора на число называются линейными операциями.
Линейные операции имеют следующие основные свойства.
Для любых векторов  ,
, 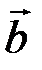 ,
, 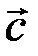 на плоскости (в пространстве) и для любых действительных чисел
на плоскости (в пространстве) и для любых действительных чисел 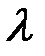 ,
, 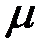 :
:
1)  ;
;
2) 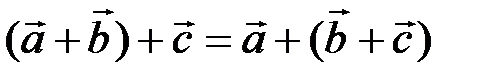 ;
;
3) 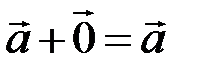 ;
;
4) 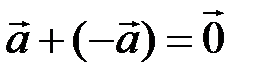 ;
;
5) 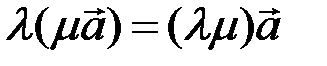 ;
;
6) 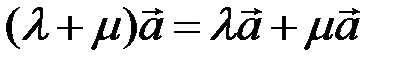 ;
;
7) 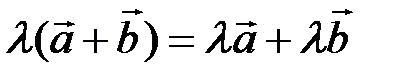 ;
;
8) 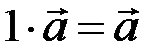 .
.
Свойства 1) – 3) позволяют определить сумму любого числа векторов, не зависящую от порядка суммирования.
Выражение  называется линейной комбинацией векторов
называется линейной комбинацией векторов 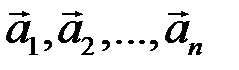 с коэффициентами
с коэффициентами 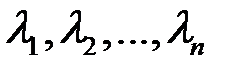 .
.
Для любых векторов  и
и 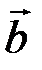 существует единственный вектор
существует единственный вектор 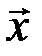 , такой что
, такой что  . Он называется разностью векторов
. Он называется разностью векторов 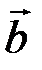 и
и  , обозначается
, обозначается 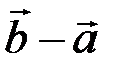 и находится по формуле
и находится по формуле 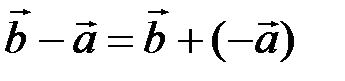 .
.
Дата публикования: 2015-09-17; Прочитано: 322 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
