 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры решения задач. 4.2.1.Пользуясь определением, найти ранги матриц
|
|
4.2.1. Пользуясь определением, найти ранги матриц
 ,
,  и
и 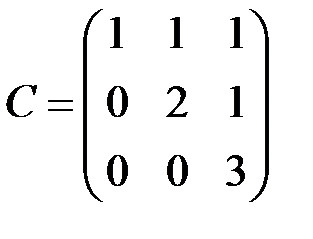 .
.
◄ 1) Так как ранг матрицы – наибольший из порядков ненулевых миноров, то надо начать с нахождения миноров самого большого порядка – второго.
Найдем минор второго порядка матрицы  , из элементов, взятых из строк с номерами 1 и 2 и столбцов с номерами 1 и 2:
, из элементов, взятых из строк с номерами 1 и 2 и столбцов с номерами 1 и 2:  . Он, увы, нулевой. Найдем еще один минор второго порядка
. Он, увы, нулевой. Найдем еще один минор второго порядка  . Он нулю не равен. Поэтому
. Он нулю не равен. Поэтому  .
.
2) У матрицы  все миноры наибольшего – второго порядка – нулевые:
все миноры наибольшего – второго порядка – нулевые:
 ,
,  и
и  .
.
Поэтому надо проверять миноры первого порядка – элементы матрицы. Например,  . Поскольку есть ненулевой минор первого порядка, а все миноры большего порядка нулевые, то
. Поскольку есть ненулевой минор первого порядка, а все миноры большего порядка нулевые, то  .
.
3) У матрицы  единственный минор наибольшего – третьего порядка
единственный минор наибольшего – третьего порядка  . Поэтому
. Поэтому  . ►
. ►
4.2.2. Найти ранг матрицы  .
.
◄ Будем делать элементарные преобразования матриц, не меняющие ранга:
 .
.
Шаг 1. Первую строку оставили неизменной, ко второй прибавили первую, умноженную на (–1), к третьей прибавили первую, умноженную на (–3), к четвертой прибавили первую, умноженную на (–2).
Шаг 2. Первую и вторую строки оставили неизменными, к третьей прибавили вторую, умноженную на (–1), к четвертой прибавили вторую, умноженную на (–2).
Шаг 3. Удалили нулевые строки.
В итоге получили  -матрицу
-матрицу  , эквивалентную матрице
, эквивалентную матрице  , у которой минор второго порядка
, у которой минор второго порядка  . Поэтому
. Поэтому  .
.
Заметим, что, если бы мы попытались найти ранг по определению, то нам бы пришлось сначала вычислить все 10 миноров четвертого порядка, которые равны нулю, потом 20 миноров третьего порядка, тоже равные нулю, пока не обнаружим ненулевой минор второго порядка. ►
4.2.3. При каких значениях параметра  линейная система
линейная система

совместна?
◄ Выпишем расширенную матрицу системы  .
.
Слева от вертикальной черты у нас выписана и основная матрица. Будем вычислять одновременно ранги обеих матриц, делая элементарные преобразования только со строками:
 .
.
Шаг 1. Первую строку оставили неизменной, ко второй прибавили первую, умноженную на (–1), к третьей прибавили первую, умноженную на (–2).
Шаг 2. Первую и вторую строки оставили неизменными, к третьей прибавили вторую, умноженную на (–1).
У преобразованной основной матрицы  можно удалить нулевую строку и ее ранг – 2. При
можно удалить нулевую строку и ее ранг – 2. При  у преобразованной расширенной матрицы тоже нулевая строка и ее ранг – 2. По теореме Кронекера-Капелли при
у преобразованной расширенной матрицы тоже нулевая строка и ее ранг – 2. По теореме Кронекера-Капелли при 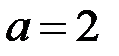 система совместна. При
система совместна. При  минор третьего порядка расширенной матрицы
минор третьего порядка расширенной матрицы
 .
.
Поэтому ранг расширенной матрицы равен 3. Он не совпадает с рангом основной матрицы. Согласно теореме Кронекера-Капелли при  система несовместна.
система несовместна.
Наши действия с расширенной матрицей можно рассматривать как прямой ход метода Гаусса (см. п. 3.1.3). При  получаем уравнение
получаем уравнение  , не имеющее решения, что влечет несовместность системы. ►
, не имеющее решения, что влечет несовместность системы. ►
Дата публикования: 2015-09-17; Прочитано: 320 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
