Алгебраическое уравнение

(4)

называется характеристическим уравнением ЛОДУ (3); оно получается из ЛОДУ (3) заменой производной степенью 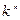[при этом ].

Напомним, что любое алгебраическое уравнение n-й степени с действительными коэффициентами над полем С комплексных чисел имеет ровно n корней с учетом кратности (некоторые из них могут и совпадать, т.е. быть кратными), причем уравнение, наряду с комплексным корнем , всегда имеет и сопряженный с ним корень .

1 случай: все корни характеристического уравнения действительные и различные

Теорема 13. Если число является корнем характеристического уравнения (4), то функция является частным решением ЛОДУ (3).

2 случай: корни характеристического уравнения действительные, но среди них есть кратные

Теорема 14. Если число является корнем характеристического уравнения (4) кратности , то функции являются линейно независимыми решениями ЛОДУ (3).

3 cлучай: среди корней характеристического уравнения есть некратные комплексные корни

Теорема 15. Некратным комплексным корням характеристического уравнения (4) соответствует пара частных решений ЛОДУ (3)

.

4 случай: среди корней характеристического уравнения есть кратные комплексные корни

Теорема 16. Комплексным корням характеристического уравнения (4) кратности соответствуют частных решений ЛОДУ (3)

2.2.2. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Метод неопределенных коэффициентов

Линейным неоднородным дифференциальным уравнением (ЛНОДУ) n-го порядка называется д.у. вида

(5)

где - заданные непрерывные на промежутке функции.

Теорема 17. Общее решение ЛНОДУ (5) есть сумма какого-либо его частного решения и общего решения соответствующего ему однородного уравнения (1).

Линейным неоднородным дифференциальным уравнением (ЛНОДУ) n-го порядка с постоянными коэффициентами называется д.у. вида

(6)

где .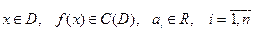

Теорема 18. (Метод неопределенных коэффициентов). Если правая часть ЛНОДУ (6) с постоянными коэффициентами имеет вид

, (7)

где - заданные многочлены степени m и n, , то ЛНОДУ (6) своим частным решением имеет функцию

, (8)

где - полные многочлены степени 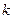, - кратность числа как корня характеристического уравнения соответствующего ЛОДУ (3).

Замечание 15. Если правая часть 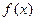данного ЛНОДУ не имеет вид (7), то иногда может помочь

Теорема 19 (Принцип наложения частных решений ЛНОДУ). Если являются решениями соответственно уравнений , то сумма является решением уравнения .

2.2.3. Линейные неоднородные дифференциальные уравнения n-го порядка. Метод вариации произвольных постоянных

Теорема 20 (Метод вариации произвольных постоянных). Если известна фундаментальная система решений соответствующего ЛОДУ (2), то общее решение ЛНОДУ (5) можно найти по формуле

,

где функции , определяются из следующей системы:

(9)

Замечание 16. Метод вариации произвольных постоянных можно применить при решении ЛНОДУ и тогда, когда: во-первых, правая часть уравнения 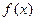имеет вид, отличный от вида (7); во–вторых, коэффициенты , могут быть переменными на промежутке D.