Уравнение Лагранжа

Д.у. 1-го порядка

,

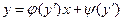где 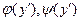- дифференцируемые функции от производно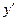й и , называется уравнением Лагранжа.

Замечание 12. Если в уравнении Лагранжа ввести параметр 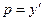, продифференцировать по 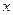и разрешить его относительно 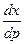, то получим уравнение

,

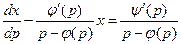которое является линейным (относительно 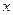и 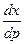) и, значит, интегрируется в квадратурах. Таким образом, метод введения параметра позволяет привести уравнение Лагранжа к д.у., разрешенному относительно производной.

Замечание 13. Д.у. 1-го порядка

,

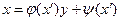где 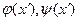- дифференцируемые функции от производно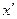й и 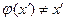, тоже называется уравнением Лагранжа.