Пример 9.1

Привести к каноническому виду уравнение второго порядка:

.

В этом уравнении

.

Подставив значения коэффициентов в инвариант , убедимся, что

,

то есть мы имеем дело с эллипсом.

Подставив значения коэффициентов в уравнения (9.20), и решив систему

,

найдем координаты центра симметрии эллипса

.

Подставив эти числа в уравнения (9.21), найдем новое значение свободного члена

.

После переноса начала координат в центр симметрии эллипса его уравнение приобретает следующий вид:

(9.26)

Перекрестный член в этом уравнении уничтожается за счет поворота осей координат. Тангенс угла поворота определяем из уравнения (9.23):

.

Коэффициенты и найдем, используя инварианты:

(Если 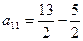, то .)

В итоге уравнение эллипса примет следующий вид:

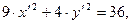или (9.27)

Рис. 9.5