 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Геометрические свойства смешанного произведения
|
|
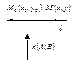 1. Модуль смешанного произведения некомпланарных векторов
1. Модуль смешанного произведения некомпланарных векторов 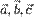 равен объему
равен объему 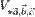 параллелепипеда, построенного на этих векторах. Произведение
параллелепипеда, построенного на этих векторах. Произведение 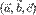 положительно, если тройка векторов
положительно, если тройка векторов 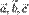 — правая, и отрицательно, если тройка
— правая, и отрицательно, если тройка 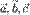 — левая, и наоборот.
— левая, и наоборот.
2. Смешанное произведение 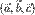 равно нулю тогда и только тогда, когда векторы
равно нулю тогда и только тогда, когда векторы 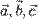 компланарны:
компланарны:
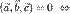 векторы
векторы 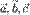 компланарны.
компланарны.
Докажем первое свойство. Найдем по определению смешанное произведение:, где 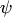 — угол между векторами
— угол между векторами 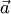 и
и 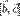 . Модуль векторного произведения (по геометрическому свойству 1) равен площади
. Модуль векторного произведения (по геометрическому свойству 1) равен площади 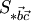 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 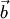 и
и  :. Поэтому
:. Поэтому 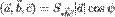 . Алгебраическое значение
. Алгебраическое значение  длины проекции вектора
длины проекции вектора 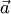 на ось, задаваемую вектором
на ось, задаваемую вектором 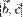 , равно по модулю высоте
, равно по модулю высоте  параллелепипеда, построенного на векторах
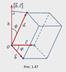
параллелепипеда, построенного на векторах 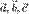 (рис. 1.47). Поэтому модуль смешанного произведения равен объему
(рис. 1.47). Поэтому модуль смешанного произведения равен объему 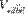 этого параллелепипеда:
этого параллелепипеда:
Знак смешанного произведения определяется знаком косинуса угла 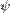 . Если тройка
. Если тройка 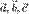 правая, то
правая, то 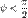 и смешанное произведение
и смешанное произведение 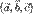 положительно. Если же тройка
положительно. Если же тройка 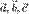 левая, то
левая, то 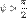 и смешанное произведение
и смешанное произведение 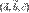 отрицательно.
отрицательно.
Докажем второе свойство. Равенство возможно в трех случаях: 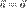 или
или 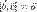 (т.е.
(т.е. 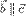 ),или
),или  (т.е. вектор
(т.е. вектор 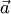 принадлежит плоскости векторов
принадлежит плоскости векторов 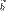 и
и  ). В каждом случае векторы
). В каждом случае векторы 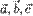 компланарны
компланарны
Критерий компланарности трёх векторов: Для того чтобы векторы 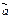 ,
, 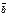 и
и  были компланарны, необходимо и достаточно, чтобы
были компланарны, необходимо и достаточно, чтобы 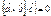 .
.
В самом деле, это означает, что объём параллелепипеда, построенного на этих векторах после приведения их к общему началу, будет равен нулю, а это возможно только когда все три вектора лежат в одной или параллельных плоскостях, т.е. компланарны.
Дата публикования: 2015-07-22; Прочитано: 246 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
