Билет 9. Векторное произведение векторов

Векторное произведение векторов

Три вектора называют упорядоченной тройкой векторов, если указано, какой из них первый, какой второй и какой третий.

Некомпланарная тройка векторов , 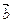и называется правой (левой) если после приведения их к общему началу расположен по ту сторону от плоскости векторов и 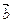, откуда наикратчайший поворот от к 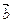кажется осуществляемым против (по) часовой стрелки.

Векторным произведение и 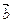называют вектор такой, что , , и векторы , и образуют правую тройку. Обозначение: ­ .

Алгебраические свойства:

1. .

2. .

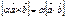3. .

4. .

Необходимое и достаточное условие коллинеарности двух векторов: Для того чтобы , необходимо и достаточно, чтобы .

1. Пусть , и ­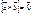 . Тогда , т.е. .

2. Пусть . Тогда .

Модуль векторного произведение равен площади параллелограмма, построенного на этих векторах.

.

Выражение векторного произведения в ДСК

Если в ДСК и то . .