Билет 8. Скалярным произведением на называется число .

Скалярное произведение

Скалярным произведением на 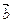называется число .

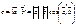Второе определение: .

Оба определения равносильны, т.к. , .

Алгебраические свойства скалярного произведения:

1. .

2. .

3. .

4. , если , иначе .

5. Геометрические свойства скалярного произведения

С помощью скалярного произведения можно находить основные метрические величины: длины отрезков (или, что то же самое, длины векторов) и величины углов.

1. Длина вектора а находится по формуле: .

2. Величина угла между ненулевыми векторами находится по формуле:

Отсюда заключаем, что:

— ненулевые векторы и перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: ;

— угол между ненулевыми векторами и острый тогда и только тогда, когда их скалярное произведение положительно;

— угол между ненулевыми векторами и тупой тогда и только тогда, когда их скалярное произведение отрицательно.

Алгебраическое значение длины ортогональной проекции вектора 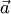на ось, задаваемую вектором.

Ортогональная проекция вектора 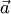на ось, задаваемую вектором.

Если ось задается единичным вектором , то. Свойства 1 и 2 следуют непосредственно из определения скалярного произведения. Третье и четвертое свойства вытекают из геометрического смысла скалярного произведения (см. (1.8)) и п.1 замечаний 1.4.

Необходимое и достаточное условие ортогональности двух векторов: Дл того чтобы и 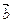были ортогональны, необходимо и достаточно, чтобы ­ .

1.Ес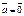ли или , то теорема справедлива, т.к. нулевой вектор имеет произвольное направление и .

1. Пусть . Тогда и, т.к. и , то , т.е. .

2. Пусть . Тогда .

Пусть задана прямоугольная декартова система координат и пусть и 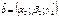. Тогда , т.к. , и .