Билет 7. Совокупность векторов, обладающих двумя свойствами: любой вектор может быть выражен через эти вектора и это выражение будет единственным

Любой вектор в пространстве может быть единственным образом разложен по трём некомпланарным векторам. Доказывается аналогично.

Совокупность векторов, обладающих двумя свойствами: любой вектор может быть выражен через эти вектора и это выражение будет единственным, называется базисом. Таким образом, базис образуют любые два неколлинеарных вектора на плоскости и любые три некомпланарных в пространстве.

Пусть - базис в пространстве и вектор . Тогда числа a, b и g называют координатами вектора в базисе .

Базис образует аффинную систему координат.

Углом между векторами называют наименьший из углов, на который надо повернуть один вектор до совмещения с другим по приведения из к общему началу. Обозначение: .

Орт оси – единичный вектор, сонаправленный с осью.

Углом между вектором и осью называют угол между вектором и ортом оси.

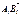- геометрическая проекция на ось l.

- скалярная проекция на ось l.

Свойства проекции вектора на ось:

1. .

2. .

3. .

Координаты вектора в прямоугольной декартовой системе координат

ДСК – частный случай аффинной системы координат.

Разложим по базису ­ , который образует декартову систему координат и центр которого совпадает с началом вектора : . Здесь x, y и z – координаты вектора в базисе. Тогда , , .

Направляющие косинусы вектора в прямоугольной декартовой системе координат

Пусть a, b и g - углы, которые образует с осями ДСК (Ox, Oy и Oz). Тогда , и называют направляющими косинусами 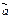. Пусть x, y и z – координаты вектора 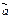в ДСК. Тогда , , , , , , .

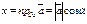Если даны две точки М1 и М2, являющиеся соответственно началом и концом вектора а, то его коорлинаты X Y Z вычисляются по вормулам X=x2-x1 Y=y2-y1 Z=z2-z1.

Формула |a|=Sqrt(X^2+Y^2+Z^2) позволяет по координатам вектора определить его модуль.

Если q w e – углы, которые состовляют вектор а с координатными осями, то cos q cos w cos e называются направляющими косинусами вектора а. Вследствии X=|a|cosq Y=|a|cosw Z=|a|cose

Отсюда следует, что cos^2q+cos^2w+cos^2e=1

Аффинная система координат (косоугольная система координат) — прямолинейная система координат в аффинном пространстве.

В -мерном пространстве она задаётся упорядоченной системой линейно независимых векторов , выходящих из одной точки . Аффинными координатами точки 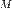называют такие числа , что

Tочку и систему векторов называют репером или аффинным базисом; прямые, проходящие через вектора — координатными осями.

На аффинной плоскости координату называют абсциссой, а — ординатой точки . В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.

Линейные операции над векторами в аффинных координатах

Пусть , .

Свойства линейных операций:

1. .

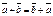2. .

3. .

4. для .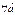

5. .

6. .

7. .

8. .

Пусть в пространстве выбран базис 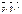и пусть и . Тогда , , , . Таким образом, , .