Способ

На прямой задана точка M₀(x_0,y₀,z₀) и известен направляющий вектор прямой

Опр. Любой вектор, параллельный данной прямой называется направляющим вектором этой прямой.

Составим уравнение прямой.

Рис.31

Возьмем на прямой произвольную точку M(x,y,z) (Рис.31). По условию векторы и 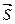коллинеарны, следовательно их координаты пропорциональны: (17).

Уравнения (17) называются каноническими уравнениями прямой в пространстве.

2 Способ.

Прямая может быть задана, как линия пересечения двух плоскостей в пространстве.

Систему из двух непараллельных плоскостей

(18) называют общим уравнением прямой в пространстве.