 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Прямая на плоскости в декартовой системе координат
|
|
На прямой берем произвольную точку M(x,y) и, используя свойства этой прямой, составляем уравнение, которому должны удовлетворять координаты этой точки. При составлении уравнения используем аппарат векторной алгебры.
Опр. Любой вектор 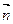 =(A,B), перпендикулярный данной прямой, называется нормальным вектором данной прямой.
=(A,B), перпендикулярный данной прямой, называется нормальным вектором данной прямой.
Опр. Любой вектор 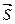 =(m,n), параллельный данной прямой, называется направляющим вектором данной прямой.
=(m,n), параллельный данной прямой, называется направляющим вектором данной прямой.
Существует два способа задания прямой линии на плоскости.
Способ 1. На прямой задана точка M0(x0,y0) и известен нормальный вектор прямой 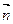 =(A,B). (Рис.1)
=(A,B). (Рис.1)
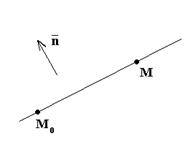
Рис.10
Пусть M(x,y) – произвольная точка прямой. Векторы 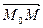 и
и 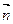 ортогональны и следовательно их скалярное произведение равно нулю. Уравнение прямой в векторной форме имеет вид:
ортогональны и следовательно их скалярное произведение равно нулю. Уравнение прямой в векторной форме имеет вид: 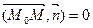 (1).В координатной: A(x-x0)+B(y-y0)=0 ( 2 )
(1).В координатной: A(x-x0)+B(y-y0)=0 ( 2 )
Уравнение (2), записанное в виде: Ax+By+C=0 ( 3 ), где C= -Ax0-By0 называется общим уравнением прямой. Заметим, что коэффициенты при x и y в общем уравнении прямой определяют координаты нормального вектора прямой.
Способ 2. На прямой задана точка M0(x0,y0) и известен направляющий вектор прямой
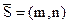 .
.
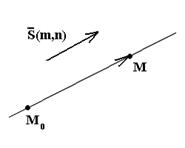
Рис.11
Возьмем на прямой произвольную точку M(x,y). Условие коллинеарности векторов 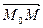 =(x-x0,y-y0) и
=(x-x0,y-y0) и 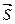 =(m,n) и будет уравнением прямой:
=(m,n) и будет уравнением прямой:
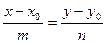 ( 4 )
( 4 )
Уравнение(4) называется каноническим уравнением прямой на плоскости.
Все задачи на составление уравнения прямой на плоскости сводятся к получению и (или) использованию уравнений (2,4).
Рассмотрим некоторые примеры:
а) Составить параметрические уравнения прямой.
Используем уравнение (4). Введем параметр 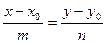 = t. Из каждого равенства выразим x и y:
= t. Из каждого равенства выразим x и y: 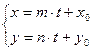 (5). Полученные уравнения и есть параметрические уравнения прямой на плоскости.
(5). Полученные уравнения и есть параметрические уравнения прямой на плоскости.
б) Составить уравнение прямой, проходящей через две заданные точки A(x1,y1) и B(x2,y2).
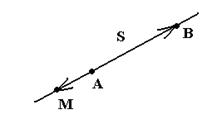
Рис. 12
Вектор 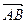 =(x2-x1,y2-y1) - направляющий вектор прямой. На прямой возьмем произвольную точку М (х, у). Векторы
=(x2-x1,y2-y1) - направляющий вектор прямой. На прямой возьмем произвольную точку М (х, у). Векторы 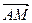 и
и 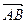 коллинеарны, и следовательно их соответствующие координаты пропорциональны:
коллинеарны, и следовательно их соответствующие координаты пропорциональны:
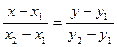 (6)
(6)
Это уравнение прямой, проходящей через две заданные точки.
в) Составить уравнение прямой, если известна точка M0(x0,y0) на прямой и угол α между прямой и осью ОХ?
Возьмем на прямой произвольную точку M(x,y) (Рис.13).
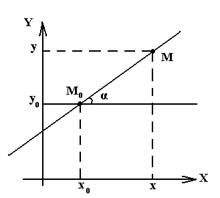
Рис.13
Из рисунка видно, что 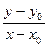 =
= 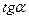 - тангенс угла между прямой и осью ОХ.
- тангенс угла между прямой и осью ОХ.
Обратимся к уравнению прямой (2) A(x-x0)+B(y-y0)=0, где А и В – координаты нормального вектора прямой. Из уравнения следует, что 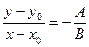
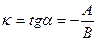 называют угловым коэффициентом прямой. Из уравнения прямой (2) получаем: y-y0=k(x-x0) ( 7 ) – уравнение прямой с угловым коэффициентом k, проходящей через точку М0. Уравнение (7) можно преобразовать к виду y=kx+b ( 8 ), где b=y0-kx0. Уравнение (8) называется уравнением прямой с угловым коэффициентом.
называют угловым коэффициентом прямой. Из уравнения прямой (2) получаем: y-y0=k(x-x0) ( 7 ) – уравнение прямой с угловым коэффициентом k, проходящей через точку М0. Уравнение (7) можно преобразовать к виду y=kx+b ( 8 ), где b=y0-kx0. Уравнение (8) называется уравнением прямой с угловым коэффициентом.
г) Записать уравнение прямой в отрезках:
Вернемся к уравнению (30 и перенесем свободный член вправо
Ax+By =-C
Разделим обе части уравнения на -С:
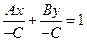
или
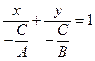
Введем обозначения
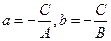
Получим 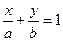 - уравнение прямой в отрезках, где а, в – величины отрезков, которые прямая отсекает на координатных осях.
- уравнение прямой в отрезках, где а, в – величины отрезков, которые прямая отсекает на координатных осях.
Задача. Заданы координаты вершины треугольника А(1,-2),В(3,-1),С(0,1). Составить уравнения:
1) стороны АС
2) высоты ВД
3) медианы ВЕ
1) 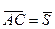 - направляющий вектор
- направляющий вектор

М(х,у) 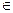 прямой
прямой
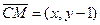
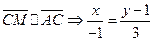 - каноническое ур-ие прямой
- каноническое ур-ие прямой
3х +у -1 =0 – общее ур-ие прямой
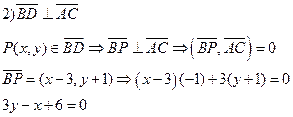
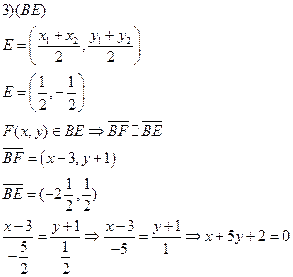
Дата публикования: 2015-07-22; Прочитано: 1542 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
