 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Условие параллельности прямой и плоскости
|
|
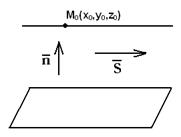
Рис. 42
Из Рис. 42 видно, что в этом случае векторы 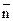 и
и 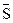 перпендикулярны, условие перпендикулярности векторов и есть условие параллельности прямой и плоскости:
перпендикулярны, условие перпендикулярности векторов и есть условие параллельности прямой и плоскости: 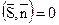 или в координатной форме:
или в координатной форме: 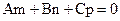 .
.
Если при этом координаты точки М0(x0,y0,z0) удовлетворяют уравнению плоскости, то прямая принадлежит этой плоскости.
Примеры решения задач.
Задача Найти точку пересечения прямой 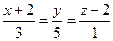 с плоскостью
с плоскостью  Решение. Координаты точки пересечения прямой с плоскостью находятся из совместного решения уравнений прямой и плоскости, т.е. из системы:
Решение. Координаты точки пересечения прямой с плоскостью находятся из совместного решения уравнений прямой и плоскости, т.е. из системы:
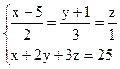
Запишем уравнения прямой в параметрической форме
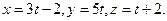 Подставим эти выражения в уравнение плоскости
Подставим эти выражения в уравнение плоскости
 Отсюда
Отсюда 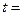 , а из параметрических уравнений прямой получим координаты точки пересечения
, а из параметрических уравнений прямой получим координаты точки пересечения 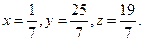
Задача. Составить уравнений прямой, проходящей через точку М0(1,2,-6) перпендикулярно плоскости 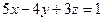 .
.
Решение.
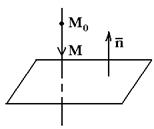
Рис. 43
Возьмем на прямой произвольную точку M(x,y,z).(Рис. 43)
Векторы 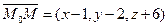 и
и 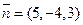 параллельны. Здесь
параллельны. Здесь 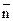 - нормальный вектор плоскости. По условию параллельности векторов
- нормальный вектор плоскости. По условию параллельности векторов 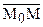 и
и 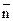
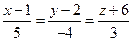 .
.
Получены канонические уравнения искомой прямой.
Задача Составить уравнение плоскости, проходящей через точку М0(5,2,-6) перпендикулярно прямой 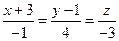 .
.
Дата публикования: 2015-07-22; Прочитано: 981 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
