Решение ДУ с помощью степенных рядов

Примеры:

1) , .

Найти частное решение .

Решение:

Искомое частное решение будем искать в виде степенного ряда по степеням 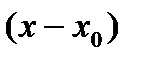, где 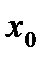- фиксированное значение аргумента х, в котором даны начальные условия.

Так как известно, что разложение функции в степенной ряд в точке 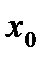и 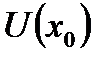является единственным и совпадает с разложением этой функции в ряд Тейлора, то известны формулы для вычисления коэффициентов:

,

,

.

…

(из начальных условий)

Из данного ДУ находим третью производную в нуле:

Для следующего коэффициента продифференцируем обе части данного ДУ по х (это можно сделать, так как в уравнение выполняется тождественно при всех х).

Продолжая дифференцирование данного ДУ можно вычислить сколько угодно , при этом, если удается обнаружить закономерность и записать общую формулу для , то можно исследовать радиус сходимости, если же закономерность не обнаруживается, то в этом случае полагают R =1 при условии, что вычисленные коэффициенты убывают.

Ответ: искомое частное решение ДУ имеет вид:

2)

Найти частное решение .

Решение:

, п= 0,1,2,..

Далее, продифференцируем искомое разложение функции дважды и подставим полученные ряды в исходное ДУ, разложив по степеням х.

Тождественное равенство двух степенных рядов означает, что совпадают их коэффициенты при одинаковых степенях х приравнивают коэффициенты при одинаковых степенях х:

Коэффициенты:

При ,

При

При

При

При

где

В общем случае:

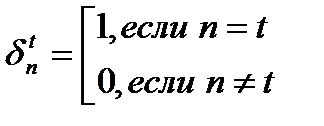(в логическом смысле)

Таким образом, для коэффициентов искомого разложения получается рекуррентная формула:

(*)

Если рекуррентную формулу для коэффициентов удается преобразовать к формуле общего , то радиус сходимости вычисляется, иначе R= 1 (если наблюдается убывание коэффициентов по модулю, начиная с какого-то номера).

Ответ: считать по рекуррентной формуле (*).