Основные свойства степенных рядов

Можно показать, что степенной ряд 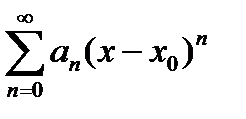имеет равномерную сходимость при всех х, таких, что , где .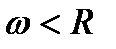

Мажорантом при этом является числовой ряд , так как и ряд сходится, так как точка 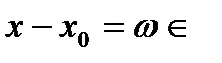области абсолютной сходимости исходного ряда.

Таким образом, степенной ряд сходится равномерно на любом отрезке, полностью лежащем внутри области абсолютной сходимости.

Для всех х из области абсолютной сходимости для степенных рядов выполняются свойства, общие для всех равномерно сходящихся рядов:

1. Сумма степенного ряда является непрерывной функцией для 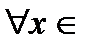области равномерной сходимости

2. Степенной ряд можно в области равномерной сходимости можно почленно дифференцировать и интегрировать, при этом дифференцируется и интегрируется его сумма, а R не изменяется(на концах промежутка при этом возможно изменение характера сходимости).