 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Список основных свойств равномерно сходящихся рядов
|
|
Если функциональный ряд 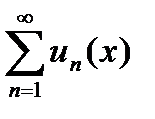 сходится к функции
сходится к функции 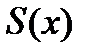 равномерно при
равномерно при 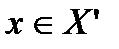 , то
, то
1. Сумма ряда 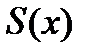 является непрерывной функцией
является непрерывной функцией 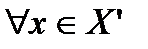
2. Функциональный ряд можно почленно интегрировать, в результате получается ряд с суммой, равной интегралу от суммы исходного ряда
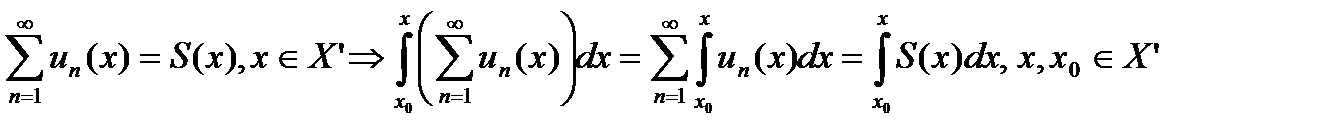
3. Если ряд 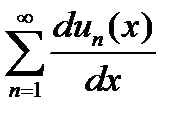 сходится равномерно для
сходится равномерно для 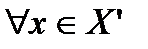 , то исходный функциональный ряд можно почленно дифференцировать,т.е.
, то исходный функциональный ряд можно почленно дифференцировать,т.е.
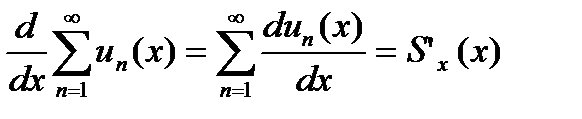
На практике для определения равномерной сходимости рядов применяется достаточный признак Вейерштрасса:
Если для функционального ряда 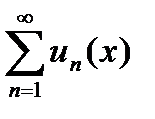 ,
, 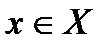 можно указать знакоположительный числовой сходящийся ряд
можно указать знакоположительный числовой сходящийся ряд 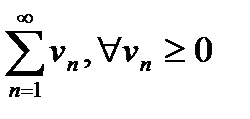 , такой, что выполняется неравенство
, такой, что выполняется неравенство 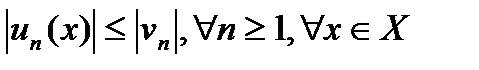 , то функциональный ряд
, то функциональный ряд 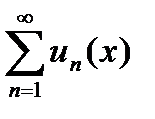 на множестве Х сходится равномерно.
на множестве Х сходится равномерно.
При этом числовой ряд 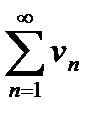 называется мажорантой для функционального ряда
называется мажорантой для функционального ряда 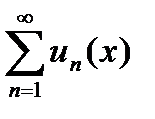 , а функциональный ряд
, а функциональный ряд 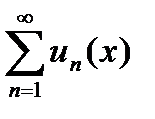 называется мажорируемым.
называется мажорируемым.
Краткая формулировка признака Вейерштрасса:
Если функциональный ряд является мажорируемым на некотором множестве, то он сходится равномерно на этом множестве.
Для мажорируемых рядов есть еще термин правильно сходящиеся ряды.
Пример:
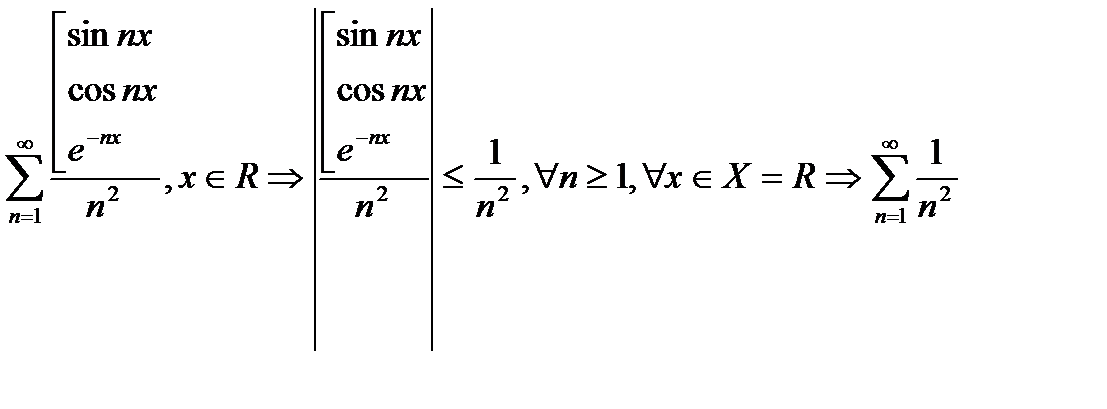 является мажорантой для данных функциональных рядов
является мажорантой для данных функциональных рядов 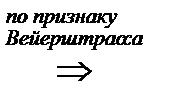 данные функциональные ряды сходятся равномерно
данные функциональные ряды сходятся равномерно 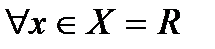 .
.
Дата публикования: 2015-07-22; Прочитано: 771 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
