Степенные ряды

Степенным рядом называется функциональный ряд,членами которого являются степенные функции с натуральным показателем (или равным нулю).

Общий вид степенного ряда:

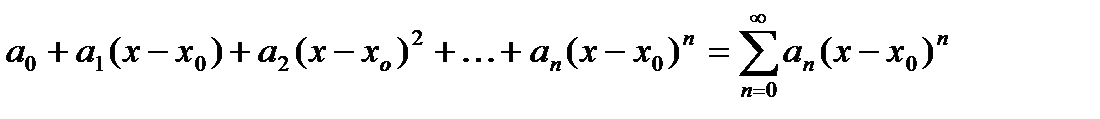
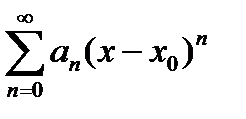- степенной ряд по степеням разности ,

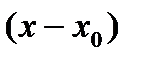где 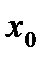- фиксированное число,

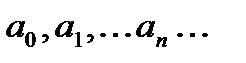называются коэффициентами степенного ряда ( числа )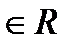

Частный случай, когда :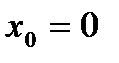

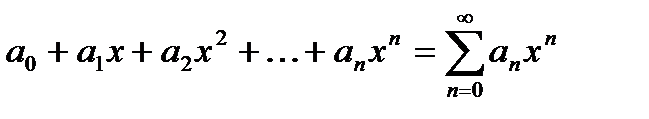- степенной ряд по степеням .

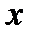Теорема Абеля (важнейшая теорема для определения области сходимости степенного ряда):

Если ряд 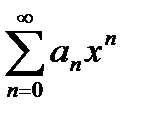сходится в точке , то он сходится, причем абсолютно, при .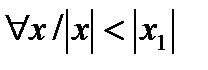

Если ряд 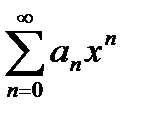расходится в точке 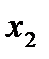, то он расходится при .

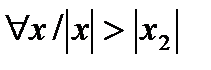Иллюстрация к теореме Абеля:

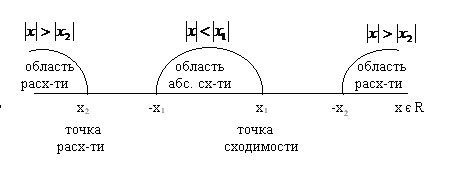
x= 0 – тривиальная точка сходимости степенного ряда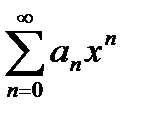

Понимание (обоснование) теоремы Абеля строится на использовании для знакоположительных числовых рядов признака сравнения в непредельной форме.

Следствие из теоремы Абеля:

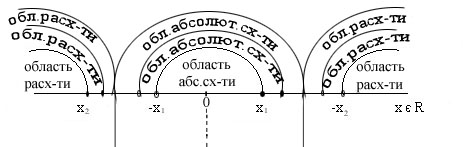
R

R – радиус сходимости степенного ряда.

Таким образом для степенного ряда 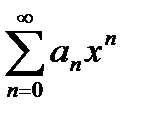можно указать число 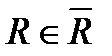, называемое радиусом сходимости, такое что область абсолютной сходимости этого ряда представляет собой интервал 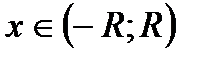, симметричный относительно 0 и длины 2 R;при этом на интервалах 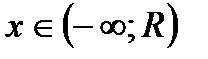и 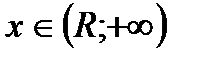ряд всегда расходится; точки 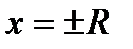(точки концов этих интервалов) нужно исследовать для каждого ряда индивидуально.

Схема области сходимости/расходимости степенного ряда 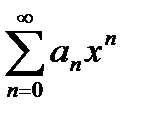(теоретическая):

Аналогично получается теоретическая схема сходимости/расходимости общего степенного ряда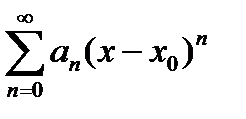

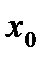- центр области сходимости.

Радиус сходимости R может оказаться:

1. R= 0

2. R= число

3. R=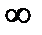

Примеры:

Определить область сходимости и область расходимости следующих степенных рядов:

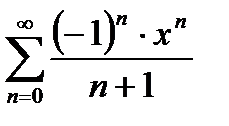
Так как степенной ряд по степеням х, то схема его области сходимости имеет вид:

Для вычисления R применим признак Даламбера к ряду, составленному из модулей членов данного ряда:

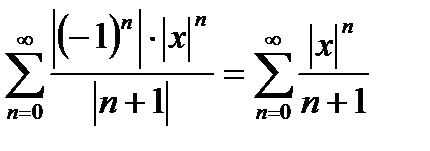
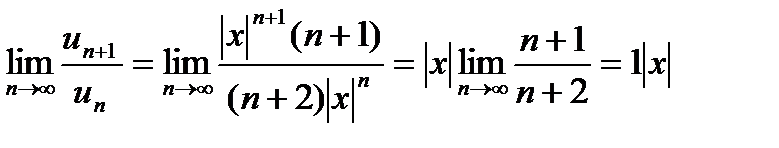
По признаку Даламбера:

Ряд из модулей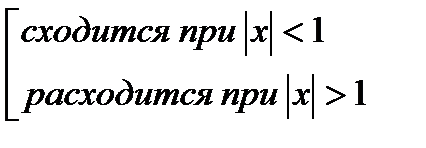

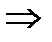исходный степенной ряд сходится абсолютно, только при 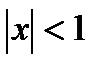(признак абсолютной сходимости).

Сравнивая получившиеся результаты с теоретической схемой, заключаем, что:

1. R =1, так как исходный ряд сходится абсолютно только при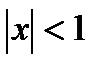

2. при 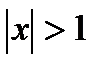абсолютной сходимости быть не может, так как расходится ряд из модулей; сравнивая со схемой, получаем, что 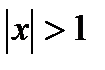- это область расходимости.

Дополнительно исследуем сходимость исходного ряда при :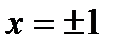

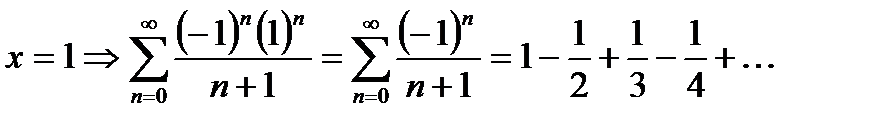- ряд Лейбница, сходится условно.

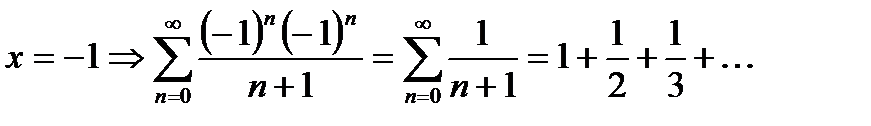- гармонический ряд, расходится.

Окончательная схема области сходимости/расходимости исходного ряда:

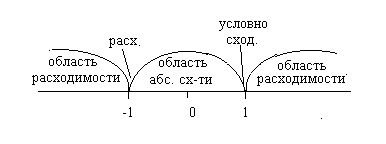
Ответ:

Замечание: если признак Даламбера или радикальный признак Коши применить к степенному ряду в общем виде 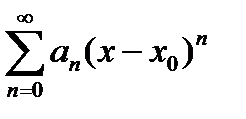, то можно получить теоретические формулы для нахождения радиуса сходимости R.

Ряд из модулей: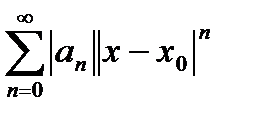

Признак Даламбера: 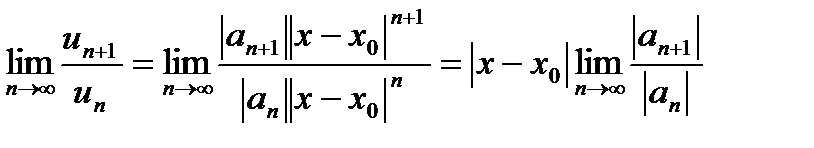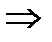ряд из модулей сходится, если 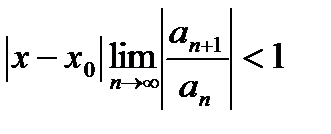или расходится, если .

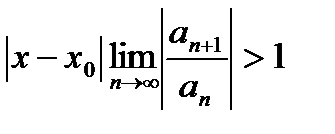Теоретическая схема области сходимости/расходимости:

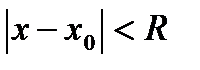
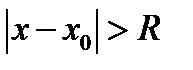
2R

Сравнивая результаты, полученные по признаку Даламбера с теоретической схемой, заключаем, что R нужно находить из условий: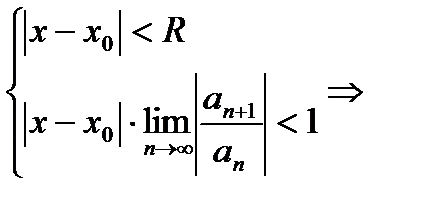

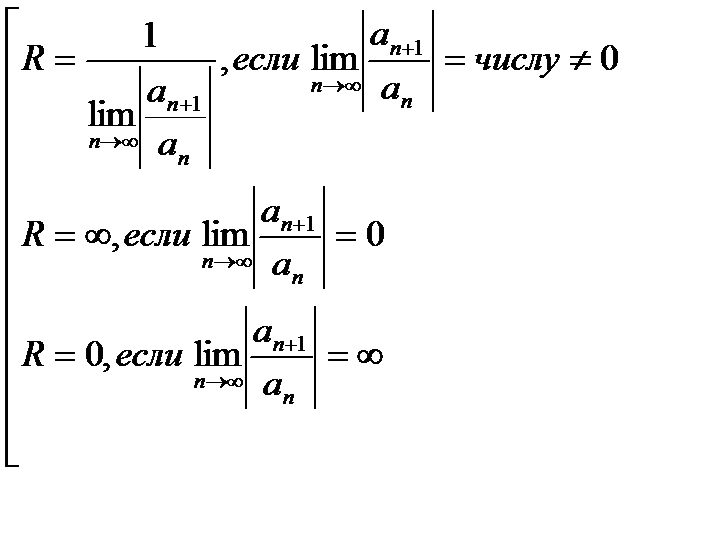
Однако выведенные формулы для R не очень удобны на практике, так как:

1. Для их применения нужно анализировать значение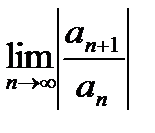

2. Для вычисления 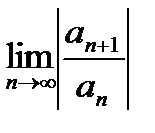нужно, чтобы все 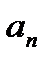были отличны от нуля.

Например, для 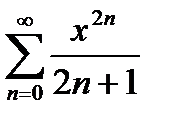применять формулы для R нельзя, так как все 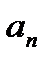(нечетные) равны 0.