Оценки остатков некоторых рядов

1)	Если знакочередующийся ряд сходится по признаку Лейбница, то модуль его остатка имеет оценку:

Для доказательства запишем знакочередующийся ряд в равернутом виде и выделим в нем частичный остаток :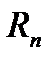

запишем 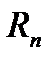иначе:

так как ряд удовлетворяет условиям Лейбница, то , поэтому все внутренние скобки положительны, следовательно, при отбрасывании этих положительных скобок получим искомую оценку:

Примеры:

Вычислим приближенное значение суммы S каждого из следующих рядов с точностью :

1) - ряд Лейбница, сходится условно;

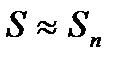, где 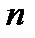нужно взять таким, чтобы соответствующий остаток . Так как ряд удовлетворяет признаку сходимости Лейбница, то

нужно взять

Ответ: 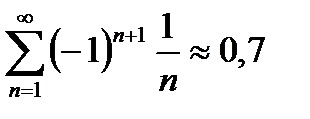или

2) - знакочередующийся ряд, удовлетворяет условиям признака Лейбница.

Таким образом

Ответ: . Заметим, что ряд сходится быстрее, чем ряд , то есть для того, что бы получить приближенное значения сумм этих рядов с одинаковой точностью, у первого ряда нужно взять меньше слагаемых, чем во втором.

2)	Если знакоположительный ряд сходится по интегральному признаку Коши, то есть сходится , где , то его остаток имеет следующую оценку: .

Пример

Вычислим приближенно с точностью сумму ряда из обратных квадратов

- сходится по интегральному признаку Коши.

вычислить 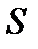с точностью 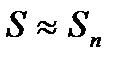, при этом

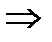
нужно взять тогда с точностью

Ответ:

Заметим, что знакоположительный ряд из обратных квадратов сходится значительно медленнее, чем соответствующий знакочередующийся ряд .

3333)

Если знакоположительный ряд сходится к признаку Даламбера, т.е. то его остаток имеет следующую оценку .

Пример

- геометрический ряд со знаменателем 0,7, сходится по признаку Даламбера, так как

Вычислим 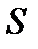с точностью

Ответ:

Замечание

1.При приближенном вычислении значения суммы ряда не нужно бояться взять лишние слагаемые в частичную сумму

2.При вычислении слагаемых в также возможны приближенные значения слагаемых; их нужно брать с большей точностью, чем вычисляется сумма ряда S (то есть нужно брать «запасные цифры после запятой»).