 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Достаточные признаки сходимости знакоположительных рядов
|
|
Числовой ряд называется знакоположительным, если все его члены являются положительными числами:
 (1)
(1)
Существует много достаточных признаков, по которым можно исследовать сходимость числовых рядов. Основными из них для знакоположительных рядов являются следующие признаки:
1) признаки сравнения (в непредельной и в предельной формах);
2) признак Даламбера (в предельной форме);
3) радикальный признак Коши;
4) интегральный признак Коши.
1. Признак сравнения в непредельной форме:
Рассматриваются два знакоположительных ряда:
 - ряд с неизвестной сходимостью, - ряд с неизвестной сходимостью,
 - ряд с известной сходимостью.
Если ряд с известной сходимостью - ряд с известной сходимостью.
Если ряд с известной сходимостью  сходится и сходится и  , то , то  тоже сходится.
Если ряд с известной сходимостью тоже сходится.
Если ряд с известной сходимостью  расходится и расходится и 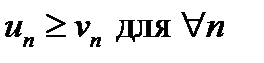 , то , то  также расходится. также расходится.
|
Другими словами:
из сходимости ряда с большими членами следует сходимость ряда с меньшими членами;
из сходимости ряда с меньшими членами следует расходимость ряда с большими членами.
 Предполагаем, что для обоих рядов необходимое условие сходимости выполняется.
Предполагаем, что для обоих рядов необходимое условие сходимости выполняется.
Для доказательства первой части признака рассматриваем сходящийся ряд  , его сумму
, его сумму  его частичные суммы
его частичные суммы  :
:
 , где
, где 
 .
.
Рассмотрим частичную сумму ряда с неизвестной сходимостью:

Так как  , то
, то  .
.
Так как существует  и
и  монотонно возрастает вследствие знакоположительности всех членов
монотонно возрастает вследствие знакоположительности всех членов  , то последовательность
, то последовательность  ограничена сверху числом
ограничена сверху числом 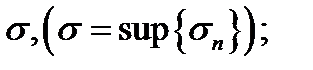
так как  для
для  , то последовательность
, то последовательность  также ограничена сверху, например, тем же числом
также ограничена сверху, например, тем же числом  .
.
Последовательность  монотонно возрастает вследствие знакоположительности всех членов
монотонно возрастает вследствие знакоположительности всех членов  . По теореме Вейерштрасса заключаем, что монотонно возрастающая и ограниченная сверху последовательность
. По теореме Вейерштрасса заключаем, что монотонно возрастающая и ограниченная сверху последовательность  имеет конечный предел. Но так как существует
имеет конечный предел. Но так как существует  , то
, то  сходится, ч.т.д.
сходится, ч.т.д.
Теперь проведем доказательство второй части:
дано  , отсюда следует, что ряд
, отсюда следует, что ряд  сходиться не может, так как в случае его сходимости из неравенства
сходиться не может, так как в случае его сходимости из неравенства  следовала бы сходимость ряда сходился бы и ряд
следовала бы сходимость ряда сходился бы и ряд  (по доказанной первой части признака). Поэтому ряд
(по доказанной первой части признака). Поэтому ряд  расходится, ч.т.д.
расходится, ч.т.д.
Замечание
Доказанный признак сравнения остается справедливым, если неравенства  или
или  выполняется при
выполняется при  , начиная с некоторого номера.
, начиная с некоторого номера.
1.1. Признак сравнения в предельной форме:
Рассматриваются два знакоположительных ряда
 ряд с неизвестной сходимостью, ряд с неизвестной сходимостью,
 ряд с известной сходимостью.
Вычисляется предел ряд с известной сходимостью.
Вычисляется предел  .
Если А – это число .
Если А – это число  , то оба ряда ведут себя одинаково в смысле сходимости (оба сходятся или расходятся). , то оба ряда ведут себя одинаково в смысле сходимости (оба сходятся или расходятся).
|
Существование такого предела гарантирует, что бесконечно малые слагаемые  и
и  имеют одинаковый порядок малости, с одинаковой скоростью стремятся к нулю, и это обеспечивает одинаковую сходимость обоих рядов.
имеют одинаковый порядок малости, с одинаковой скоростью стремятся к нулю, и это обеспечивает одинаковую сходимость обоих рядов.
Для применения признаков сравнения нужно знать ряды, сходимость которых считается известной; к таким рядам с известной сходимостью будем относить следующие ряды:
а)  геометрический ряд (q >0),
геометрический ряд (q >0),
сходится, если  ; расходится, если
; расходится, если  ;
;
б)  - гармонический ряд (расходится)
- гармонический ряд (расходится)
в)  - обобщенный гармонический ряд (ряд Дирихле),
- обобщенный гармонический ряд (ряд Дирихле),
сходится, если параметр  ; расходится, если
; расходится, если  ;
;
в’)  - ряд из обратных квадратов (сходится, так как
- ряд из обратных квадратов (сходится, так как
является рядом Дирихле с  ).
).
Примеры:
Исследуем сходимость следующих числовых рядов по признаку сравнения:
1)  ;
;
так как  при
при  и ряд
и ряд  сходится, потому что является геометрическим рядом с
сходится, потому что является геометрическим рядом с  , то данный ряд
, то данный ряд  также сходится;
также сходится;
2)  ;
;
имеем очевидное неравенство  при
при  ряд
ряд  сходится, так как это ряд из обратных квадратов; поэтому данный ряд тоже сходится;
сходится, так как это ряд из обратных квадратов; поэтому данный ряд тоже сходится;
3)  ;
;
этот ряд расходится, так как его члены удовлетворяют неравенству:
 при
при  и ряд
и ряд  расходится, потому что является гармоническим (без первого члена);
расходится, потому что является гармоническим (без первого члена);
4)  ;
;
для членов этого ряда затруднительно написать неравенство с членами какого-нибудь ряда с известной сходимостью; но заметив, что члены этого ряда имеют одинаковый порядок малости с величинами  , применим признак сравнения в предельной форме с гармоническим рядом
, применим признак сравнения в предельной форме с гармоническим рядом  :
:
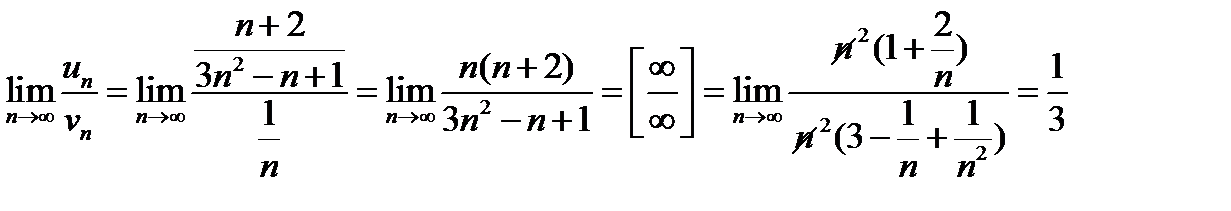 - число≠0
- число≠0
⇒данный ряд расходится, так как расходится гармонический ряд.
2 .Признак Даламбера
Для знакоположительного ряда вычисляют предел отношения последующего членов к предыдущему:  Если
Если 
|
Примеры:
Исследуем сходимость следующих знакоположительных рядов по признаку Даламбера:
1)  ;
;
Вычисляем предел отношения последующего члена ряда к предыдущему:

так как получилось, что q =0, то ряд из обратных факториалов  сходится;
сходится;
2) 



данный ряд расходится;
3) 


ответ о сходимости данного ряда по признаку Даламбера дать нельзя.
3 .Радикальный признак Коши
Для знакоположительного ряда вычисляют предел корня n- й степени из общего члена ряда:  Если
Если 
|
Примеры:
Исследуем сходимость следующих знакоположительных рядов по радикальному признаку Коши:
1) 



 данный ряд сходится;
данный ряд сходится;
2) 

Так как величина  положительная, то вычисляем предел её логарифма:
положительная, то вычисляем предел её логарифма:

переставляя теперь знаки lim и ln, получим, что:

ответ сходимости гармонического ряда  по радикальному признаку Коши дать нельзя.
по радикальному признаку Коши дать нельзя.
4 .Интегральный признак Коши
Для знакоположительного ряда  вводится функция вводится функция 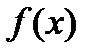 такая, что такая, что  Рассматривается несобственный интеграл от этой функции:
Рассматривается несобственный интеграл от этой функции:  ;
Если несобственный интеграл:
сходится, то сходится и ряд;
расходится, то расходится и ряд. ;
Если несобственный интеграл:
сходится, то сходится и ряд;
расходится, то расходится и ряд.
|
 Доказательство признака проводится на основании геометрической трактовки несобственного интеграла I рода
Доказательство признака проводится на основании геометрической трактовки несобственного интеграла I рода  и его сходимости/расходимости.
и его сходимости/расходимости.
Если  где где  сходится, то площадь F под кривой сходится, то площадь F под кривой  можно вычислить;
если можно вычислить;
если  расходится, то вычислить F нельзя. расходится, то вычислить F нельзя.
|
Используем эту трактовку для  , связанной с рядом, для которой
, связанной с рядом, для которой  при n= 1,2,3…:
при n= 1,2,3…:
Если числовой ряд записать в виде:

то его можно трактовать как площадь неограниченной справа ступенчатой фигуры, состоящей из прямоугольников с основанием равным 1 и высотами, равными  .
.
Если интеграл  расходится, то площадь F вычислена быть не может, поэтому не может быть вычислена и площадь бесконечной ступенчатой фигуры, изображенной на левом рисунке, так как она больше площади F; следовательно, ряд
расходится, то площадь F вычислена быть не может, поэтому не может быть вычислена и площадь бесконечной ступенчатой фигуры, изображенной на левом рисунке, так как она больше площади F; следовательно, ряд 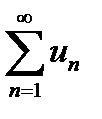 также расходится.
также расходится.
Если несобственный интеграл  сходится и равен числу F, то ряд удобно трактовать как площадь входящей в F ступенчатой фигуры, отделив для этого первый член ряда (смотри рисунок справа):
сходится и равен числу F, то ряд удобно трактовать как площадь входящей в F ступенчатой фигуры, отделив для этого первый член ряда (смотри рисунок справа):
 , очевидно, что сумма в скобках может быть выражена числом, меньшим чем F; поэтому сумма знакоположительного ряда есть и выражается некоторым числом.
, очевидно, что сумма в скобках может быть выражена числом, меньшим чем F; поэтому сумма знакоположительного ряда есть и выражается некоторым числом.
Таким образом получено неравенство  , которое и означает сходимость числового ряда.⊲
, которое и означает сходимость числового ряда.⊲
Примеры:
Исследуем сходимость следующих рядов, применяя интегральный признак Коши:
1) гармонический ряд: 

Рассмотрим несобственный интеграл: 
 несобственный интеграл расходится, следовательно, расходится и гармонический ряд;
несобственный интеграл расходится, следовательно, расходится и гармонический ряд;
2) ряд из обратных квадратов:

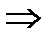
 - непрерывная и монотонно убывающая функция при
- непрерывная и монотонно убывающая функция при 
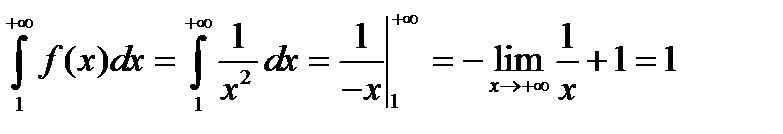
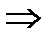 несобственный интеграл сходится, следовательно, ряд из обратных квадратов также сходится.
несобственный интеграл сходится, следовательно, ряд из обратных квадратов также сходится.
3)  - обобщенный гармонический ряд (ряд Дирихле)
- обобщенный гармонический ряд (ряд Дирихле)
Очевидно, что при p <0 члены данного ряда монотонно возрастают, а при p =0 остаются все равными 1, поэтому при 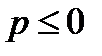
 , следовательно, ряд Дирихле расходится, так как для него не выполняется необходимое условие сходимости.
, следовательно, ряд Дирихле расходится, так как для него не выполняется необходимое условие сходимости.
Далее рассматриваем случаи  , для них необходимое условие сходимости выполняется (
, для них необходимое условие сходимости выполняется ( ), поэтому ряд может сходиться;
), поэтому ряд может сходиться;
вводим функцию  - непрерывную и монотонно убывающую при
- непрерывную и монотонно убывающую при  и рассматриваем от неё несобственный интеграл:
и рассматриваем от неё несобственный интеграл:

на основании интегрального признака Коши заключаем, что ряд Дирихле сходится при  и расходится при
и расходится при 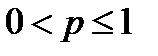 .
.
Для ответа собираем все случаи проведенного исследования:
обобщенный гармонический ряд 

При практическом исследовании числовых рядов на сходимость
рекомендуется проводить работу по следующей схеме:
- указать тип ряда  ;
;
- проверить необходимое условие 
если условие 
- для ряда, который может сходиться, подбирать достаточное условие в соответствии с типом ряда; обычно ответ можно получить по нескольким достаточным признакам;
применять достаточное признаки можно перебором до получения ответа.
Примеры:
1.  - знакоположительный ряд;
- знакоположительный ряд;
необходимое условие:

 ряд может сходиться.
ряд может сходиться.
Покажем, что сходимость данного ряда может быть получена по нескольким достаточным признакам.
Признак Даламбера:

Признак сравнения в непредельной форме:

Ряд  сходится, так как это обобщенный гармонический ряд с
сходится, так как это обобщенный гармонический ряд с  , следовательно исходный ряд сходится по признаку сравнения в непредельной форме.
, следовательно исходный ряд сходится по признаку сравнения в непредельной форме.
2.  - ряд знакоположительный;
- ряд знакоположительный;
необходимый признак сходимости:



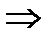

ряд может сходиться.
Покажем, что для данного ряда ответ о сходимости можно получить по признаку сравнения в предельной форме или по интегральному признаку Коши, а по признаку Даламбера получить ответ нельзя.
Признак сравнения в предельной форме:
выберем для сравнения гармонический ряд  , расходимость которого известна, и вычислим предел отношения членов обоих рядов:
, расходимость которого известна, и вычислим предел отношения членов обоих рядов:
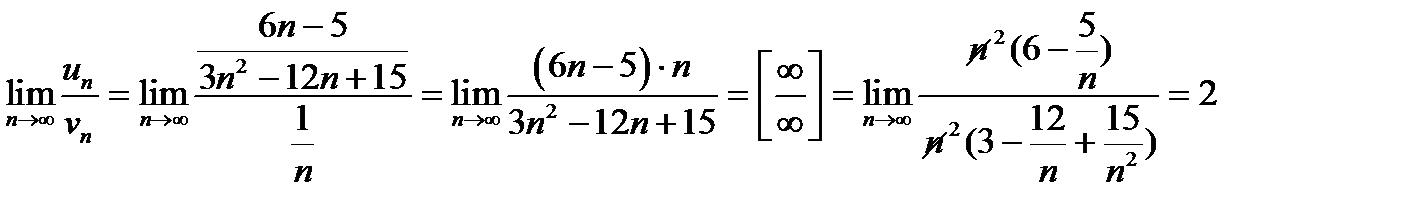
 данный ряд так же расходится как и гармонический ряд.
данный ряд так же расходится как и гармонический ряд.
Интегральный признак Коши:

 несобственный интеграл расходится, следовательно, расходится и ряд.
несобственный интеграл расходится, следовательно, расходится и ряд.
Признак Даламбера:


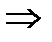 ответ о сходимости исследуемого ряда по признаку Даламбера дать нельзя.
ответ о сходимости исследуемого ряда по признаку Даламбера дать нельзя.
Упражнения для самостоятельной работы
Задача 1
Исследуйте сходимость следующих знакоположительных рядов, используя необходимый и один из достаточных признаков сходимости:
1) 
| 2) 
| 3) 
|
4) 
| 5) 
| 6) 
|
7) 
| 8) 
| 9) 
|
10) 
| 11) 
|
Ответы к упражнениям для самостоятельной работы
Задача 1
1)сходится (по признакам сравнения);
2)сходится (по признаку Даламбера);
3)расходится (по признакам сравнения);
4)расходится (по признакам сравнения или по интегральному признаку Коши);
5)сходится (по признаку Даламбера);
6)сходится (по радикальному признаку Коши);
7)расходится (т.к. не выполняется необходимое условие сходимости);
8)расходится (т.к. не выполняется необходимое условие сходимости);
9)расходится (по признакам сравнения или по интегральному признаку Коши);
10)расходится (по интегральному признаку Коши);
11)сходится (по интегральному признаку Коши).
Дата публикования: 2015-07-22; Прочитано: 2052 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
