Достаточные признаки сходимости знакопеременных рядов. Абсолютная и условная сходимости

Числовой ряд называется знакопеременным, если его членами являются как положительные, так и отрицательные числа.

Частным случаем знакопеременного ряда является ряд знакочередующийся, у которого знаки членов ряда чередуются.

(1)

Для любых знакопеременных рядов будем работать с одним достаточным признаком – признаком абсолютной сходимости;

для знакочередующихся рядов, кроме этого признака, будем еще использовать достаточный признак Лейбница.

Признак абсолютной сходимости:

Пусть дан знакопеременный ряд . Если сходится знакоположительный ряд, составленный из модулей членов данного ряда: , то сходится и данный знакопеременный ряд.

Для доказательства введем обозначения для частичных сумм обоих рядов:

Так как ряд из модулей сходится, то существует конечный предел .

В сумме введем дополнительные обозначения:

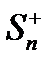- это сумма всех положительных слагаемых,

- это сумма модулей всех отрицательных слагаемых.

Тогда .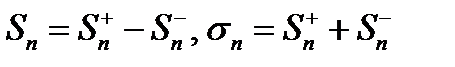

Обе величины 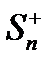и монотонно возрастают, так как состоят и положительных слагаемых, и каждая из них меньше .

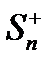Последовательность является ограниченной, так как имеет конечный предел; поэтому являются ограниченными последовательности и , так как < и < .

Таким образом, для последовательностей и выполняются условия ограниченности и монотонного возрастания, следовательно, по теореме Вейерштрасса, каждая из них является сходящейся. По теореме о разности сходящихся последовательностей заключаем, что существует конечный предел Это и доказывает утверждение о сходимости знакопеременного ряда.

Примеры:

Исследуем сходимость следующих знакопеременных рядов по достаточному признаку абсолютной сходимости:

1) - знакопеременный ряд, так как может быть и положительным и отрицательным при различных n;

Составим ряд из модулей членов данного ряда: - знакоположительный ряд,

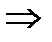
Так как сходится, то и ряд из модулей сходится (по признаку сравнения в непредельной форме) исходный ряд сходится по признаку абсолютной сходимости.

2) - знакопеременный (точнее знакочередующийся) ряд, который сходится по признаку абсолютной сходимости, так как сходится ряд из модулей его членов .

3) - знакочередующийся ряд,

ряд из модулей его членов расходится, поэтому сделать вывод о сходимости данного знакочередующегося ряда по признаку абсолютной сходимости нельзя.

1. Достаточный признак Лейбница (для знакочередующихся рядов):

Если для членов знакочередующегося ряда где выполнены два условия: то знакочередующийся ряд сходится.

Для доказательства запишем в развернутом виде знакочередующийся ряд и составим его частичные суммы с четными номерами n:

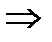
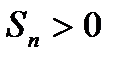и монотонно возрастает;

эти же частичные суммы можно записать иначе:

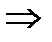
таким образом последовательность частичных сумм с четными номерами удовлетворяет условиям ограниченности: монотонно возрастает, поэтому по теореме Вейерштрасса заключаем, что существует конечный предел n -четное. Теперь рассмотрим частичные суммы нечетными номерами, которые можно представить сложением ближайшей частичной суммы с четным номером и еще одного слагаемого:

;

Следовательно, последовательность частичных сумм с нечетными номерами сходится к тому же пределу S.

Таким образом ряд сходится по определению сходимости.

Замечание

В формулировке признака Лейбница условие монотонного убывания членов ряда может выполняться, начиная с некоторого номера

Примеры:

Исследуем следующие знакочередующиеся ряды по признаку Лейбница:

1) - этот ряд называется рядом Лейбница;

проверяем для него требования признака Лейбница:

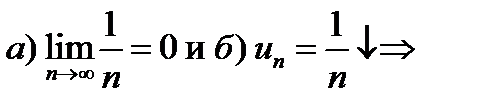ряд сходится.

2)

Проверяем выполнение условий признака Лейбница:

а)

б) монотонное убывание членов проверяем с помощью производной, сделав мысленно расширение натуральных значений n на множество действительных чисел

Таким образом, оба условия признака Лейбница выполняются, поэтому данный знакочередующийся ряд сходится.