Числовые ряды. Определение. Сходимость. Расходимость. Необходимый признак сходимости

Тема 1. Числовые и степенные ряды.

Ряд – это сумма бесконечного количества слагаемых

Числовой ряд – это сумма бесконечного количества слагаемых, являющихся числами.

(1)

- общий член ряда

Примеры:

1) 1+1+…+1+…

2)

(геометрический ряд со знаменателем q)

3) (гармонический ряд)

4) (знакочередующийся ряд)

5) (знакопеременный ряд)

n-я частичная сумма ряда ( 1 ) – это сумма первых его n слагаемых, то есть:

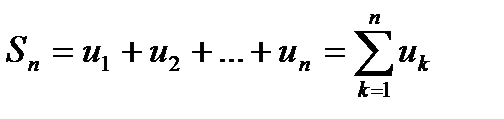
последовательность частичных сумм :

Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм; в противном случае ряд (1) называется расходящимся.

Если , то ряд является сходящимся, при этом число S называется суммой ряда.

Если , то ряд является расходящимся и суммы не имеет.

Примеры:

1) =

ряд сходится и его сумма равна 2, то есть .

Аналогично для любого геометрического ряда с :

,

2) =

расходится и суммы не имеет.

Аналогично для любого геометрического ряда с :

,

3)

ряд расходится

4) =

ряд расходится.

5)

можно сделать предположение, что

Докажем это предположение методом математической индукции:

a) если n =1, то

b) пусть верно, что ,

вычислим =

на основании метода математической индукции заключаем, что формула верна при .

Вычисляем ряд сходится и его сумма равна 1.

6)

Прежде, чем вычислять , разложим рациональную дробь на простейшие дроби:

при

Теперь вычисляем частичные суммы данного ряда:

n-ый частичный остаток ряда ( 1 ) – это ряд, который получается из ряда (1) отбрасыванием первых n слагаемых, то есть:

Очевидно, что ряд (1) можно представить сложением его n -й частичной суммы и n-го частичного остатка:

Если ряд сходится, то при , где S – это сумма ряда; при этом очевидно, что при ;

поэтому и погрешность этого равенства, равная уменьшается с увеличением n.

Отсюда следует, что сумма сходящегося ряда S может быть вычислена приближенно с любой наперед заданной точностью , для этого нужно только уметь получить оценку для остатка ряда :

с точностью , если .

Сходимость и расходимость числовых рядов устанавливается на практике с помощью необходимого и достаточных признаков.

Необходимый признак сходимости любых рядов:

Если ряд сходится, то предел его общего члена равен нулю: .

Пусть ряд сходится; это означает, что существует конечный предел последовательности его частичных сумм, то есть существует:

, где .

Тогда очевидно, что , где , так как -это последовательность тех же частичных сумм ряда с запаздывающим индексом на единицу.

Используя частичные суммы и , можно записать общий член ряда :

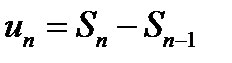, можно записать общий член ряда :

Заметим, что ряд с общим членом, не стремящимся к нулю, сходиться не может.

Потому, начиная исследовать любой числовой ряд 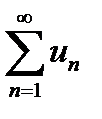по необходимому признаку сходимости, можем получить один из следующих двух результатов:

Примеры:

1) -ряд расходится, так как сходиться не может, потому что если предположить сходимость, то получаем противоречие с необходимым условием;

2) - ряд может сходиться, так как , то есть необходимое условие сходимости выполнено;

3) -ряд расходится, так как , то есть ряд расходится потому, что не выполняются необходимые условия сходимости.

Замечание.

Если члены ряда могут быть как положительными, так и отрицательными, то при проверке необходимого условия сходимости вычисляют предел общего члена ряда, взятого по модулю:

, так как в случае будет и .

Из доказательства необходимого признака сходимости рядов не следует, что этот признак является также и достаточным. В подтверждение его недостаточности можно привести пример гармонического ряда

,

Который расходится, хотя необходимый признак сходимости для него выполняется.

Доказательство расходимости гармонического ряда можно провести следующим образом. Напишем подробнее гармонический ряд:

(*)

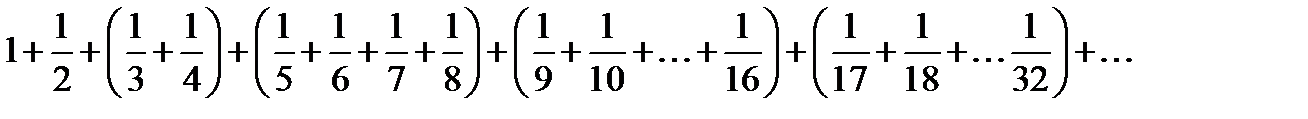Теперь составим вспомогательный ряд, который будет отличаться от гармонического ряда тем, что в каждой скобке выражения (*) все слагаемые будут заменены на меньшее из них:

(**)

Так как каждый член гармонического ряда (*) больше или равен члену с таким же номером составленного ряда (**), то для их частичных сумм и верно неравенство:

при .

Частичные суммы ряда (**) легко вычисляются при :

Таким образом показано, что частичные суммы составленного ряда (**) при достаточно больших k становятся сколь угодно большими; это обозначает, что 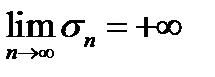. Но тогда , так как . Теперь на основании определения расходящегося ряда заключаем, что гармонический ряд 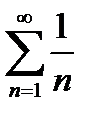расходится.