 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Применение степенных рядов
|
|
Возможность разложения функции в степенной ряд позволяет существенно упростить многие математические операции: вычисление приближенных значений данной функции, дифференцирование, интегрирование, поскольку степенной ряд можно заменить многочленом (с учетом того, что оценка остатка ряда не превысит заданного значения погрешности). В частности, можно приближенно вычислять «неберущиеся» интегралы, находить приближенные решения дифференциальных уравнений и т.д.
Рассмотрим вычисление интегралов с помощью рядов.
Примеры.
1. Для вычисления интеграла 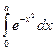 разложим подынтегральную функцию в ряд Тейлора, используя разложение функции ех:
разложим подынтегральную функцию в ряд Тейлора, используя разложение функции ех: 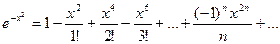
Тогда 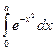 =
= 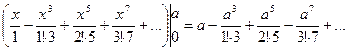
С помощью этого равенства можно вычислить рассматриваемый интеграл при любом а с любой заданной точностью.
2. Вычислим интеграл 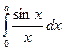 , для чего разложим функцию
, для чего разложим функцию 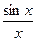 в ряд:
в ряд:
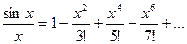 - ряд, сходящийся при любом х. Интегрируя почленно, получим:
- ряд, сходящийся при любом х. Интегрируя почленно, получим: 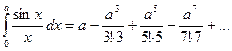
Приближенное решение дифференциального уравнения второго порядка 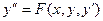 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 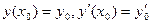 .
.
Если предположить, что решение имеет вид: 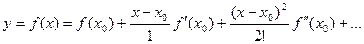 , то требуется найти значения производных
, то требуется найти значения производных 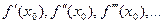 от частного решения при х = х0. Из начальных условий следует, что
от частного решения при х = х0. Из начальных условий следует, что 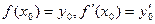 . Тогда из исходного уравнения получаем, что
. Тогда из исходного уравнения получаем, что 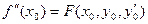 . Дифференцируя обе части исходного уравнения по х, найдем:
. Дифференцируя обе части исходного уравнения по х, найдем: 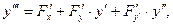 откуда можно определить
откуда можно определить 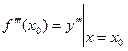 и т.д.
и т.д.
Пример. Найти решение уравнения 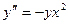 при
при 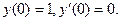
Решение: 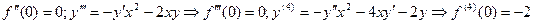 и т.д.
и т.д.
Можно получить общую формулу для производных любого порядка:
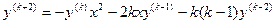 . При х = 0 эта формула дает
. При х = 0 эта формула дает
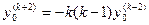 .
.
Так как 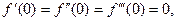 то в нуль обращаются все производные, порядок которых не кратен четырем. В конечном счете решение имеет вид:
то в нуль обращаются все производные, порядок которых не кратен четырем. В конечном счете решение имеет вид:
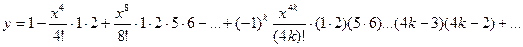
Дата публикования: 2015-07-22; Прочитано: 275 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
