Разложение в степенной ряд некоторых элементарных функций

1. . абсолютно сходится при любом х.

2. .

3. .

Используя формулу Даламбера для определения радиуса сходимости, найдем, что он равен бесконечности, то есть функции y = sin x и y = cos x раскладываются в ряд Тей-лора на всем множестве действительных чисел.

4. 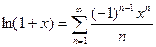. Запишем остаточный член этой формулы в форме Лагранжа:

, и исследуем его поведение при для | x| < 1,

| x | > 1 и | x | = 1. При | x| < 1 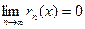, при | x | > 1 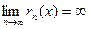. Поэтому по теореме 1.5 при | x| < 1 ряд сходится, а при | x | > 1 расходится. При х = -1 ряд расходится, так как представляет собой гармонический ряд, все члены которого имеют знак «-», а при х = 1 получаем знакопеременный ряд, сходящийся условно по признаку Лейбница. Следовательно, областью сходимости полученного ряда является интервал (-1, 1].

5. . Найдем радиус его сходимости по формуле Даламбера: Следовательно, интервал сходимости – (-1, 1).