Тема 3.3. Знакопеременные ряды. Абсолютная и условная сходимости. Признак Лейбница. Свойства абсолютно сходящихся рядов

Для числовых рядов, члены которых имеют разные знаки, задаются два вида сходимости.

Определение 3.1. Ряд называется абсолютно сходящимся, если сходится ряд из его модулей, то есть ряд .

Теорема 3.1.. Если ряд абсолютно сходится, то он сходится и в обычном смысле, то есть существует конечный предел его частичных сумм.

Доказательство.

Пусть s_n = u ₁ + u ₂ +…+ u_n, s`_n – сумма всех положительных членов среди первых п членов данного ряда, s``_n – сумма модулей всех отрицательных членов среди них. Если обозначить σ _n = |u ₁| + | u ₂| +…+ | u_n|, то

s_n = s`<sub>n</sub> – s``<sub>n</sub>, σ<sub>n</sub> = s`_n + s``_n.

Так как по условию теоремы σ_п имеет предел σ, а s`<sub>n</sub> и s``<sub>n</sub> – положительные возрастающие величины, меньшие σ, то они тоже имеют пределы s` и s``. Следовательно,

,

то есть знакопеременный ряд сходится.

Замечание. Так как ряд является знакоположительным, то для исследования знакопеременного ряда на абсолютную сходимость мы можем использовать все известные признаки сходимости знакоположительных рядов.

Пример. Для ряда 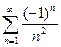ряд из модулей имеет вид . Такой ряд сходится (см. пример из лекции 1), поэтому рассматриваемый ряд сходится абсолютно.

Определение 3.2. Если ряд, составленный из модулей членов данного ряда, расходится, а сам данный ряд сходится, то говорят, что он сходится условно.