Ряды с неотрицательными членами

Пусть для всех членов ряда (1.1) выполнено условие u_n ≥ 0.

Теорема 1.6 (критерий сходимости). Ряд с неотрицательными членами сходится тогда и только тогда, когда его частичные суммы ограничены сверху.

Доказательство.

1) Если ряд сходится, то , но , то есть последовательность частичных сумм является возрастающей. Следовательно, 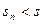, то есть { s_n } ограничена сверху числом s.

2) Пусть { s_n } ограничена сверху. Обозначим через s верхнюю грань { s_n }. Тогда, так как { s_n } возрастает, то есть число s является пределом { s_n }, следовательно, ряд сходится.