Свойства абсолютно сходящихся рядов

Теорема 3.3. Если ряд абсолютно сходится, то любой ряд, составленный из членов данного ряда, взятых, возможно, в другом порядке, тоже абсолютно сходится и имеет ту же сумму.

Доказательство. Рассмотрим ряд , составленный из членов ряда . Так как ряд сходится, можно найти номер N такой, что | s_N – s | < . Выберем теперь номер М такой, что частичная сумма содержала все слагаемые, входящие в сумму s_N. Тогда для любого m > M частичную сумму можно представить в виде:

.

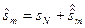Тогда в будут входить только слагаемые с номерами, большими N, поэтому

.

Тогда при т > M получаем:

Следовательно, , то есть ряд сходится, и сумма его равна s.

Проводя подобные рассуждения для ряда , можно доказать и абсолютную сходимость ряда .

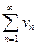Теорема 3.4 (без доказательства). Если ряды и абсолютно сходятся, то ряд, составленный из всевозможных попарных произведений u_mv_n членов этих рядов, тоже абсолютно сходится, и его сумма равна произведению сумм исходных рядов.

Замечание. Указанные свойства справедливы только для абсолютно сходящихся рядов. Если ряд сходится условно, то перестановкой его членов можно изменять сумму ряда (теорема Римана) или получить расходящийся ряд. В частности, расходящимися в этом случае будут ряды, составленные из всех положительных и из всех отрицательных членов данного условно сходящегося ряда.

Тема 3.4 Степенные ряды. Теорема Абеля. Область сходимости степенного ряда. Радиус сходимости. Основные свойства степенных рядов: равномерная сходимость, непрерывность и бесконечная дифференцируемость суммы. Почленное интегрирование и дифференцирование степенных рядов.

Определение 5.1. Степенным рядом называется функциональный ряд вида

(5.1)

Замечание. С помощью замены х – х₀ = t ряд (5.1) можно привести к виду , поэтому все свойства степенных рядов достаточно доказать для рядов вида

(5.2)

Теорема 5.1 (1-я теорема Абеля). Если степенной ряд (5.2) сходится при х = х₀, то при любом x: | x| < |x₀| ряд (5.2) сходится абсолютно. Если же ряд (5.2) расходится при х = х₀, то он расходится при любом x: | x| > |x₀|.

Доказательство.

Если ряд сходится, то поэтому существует константа с > 0:

. Следовательно, , а ряд при | x |<| x₀ | сходится, так как является суммой бесконечно убывающей геометрической прогрессии. Значит, ряд при | x |<| x₀ | абсолютно сходится.

Если известно, что ряд (5.2) расходится при х = х₀, то он не может сходиться при | x| > |x₀|, так как из ранее доказанного при этом следовало бы, что он сходится и в точке х₀.

Таким образом, если найти наибольшее из чисел х₀ > 0 таких, что (5.2) сходится при х = х₀, то областью сходимости данного ряда, как следует из теоремы Абеля, будет интервал (- х₀, х₀), возможно, включающий одну или обе границы.

Определение 5.2. Число R ≥ 0 называется радиусом сходимости степенного ряда (5.2), если этот ряд сходится, а расходится. Интервал (-R, R) называ-ется интервалом сходимости ряда (5.2).

Примеры.

1) Для исследования абсолютной сходимости ряда применим признак Далам-бера: . Следовательно, ряд сходится только при х = 0, и радиус его сходимости равен 0: R = 0.

2) Используя тот же признак Даламбера, можно показать, что ряд сходится при любом х, то есть

3) Для ряда по признаку Даламбера получим:

Следовательно, при –1 < x < 1 ряд сходится, при x < -1 и x > 1 расходится. При х = 1 получаем гармонический ряд, который, как известно, расходится, а при х = -1 ряд сходится условно по признаку Лейбница. Таким образом, радиус сходимости рассматриваемого ряда R = 1, а интервал сходи-мости – [-1, 1).

Формулы для определения радиуса сходимости степенного ряда.

1. Формула Даламбера.

Рассмотрим степенной ряд и применим к нему признак Даламбера: для сходимости ряда необходимо, чтобы .Если существует , то область сходимости определяется неравенством , то есть

- (5.3)

- формула Даламбера для вычисления радиуса сходимости.

2. Формула Коши-Адамара.

Используя радикальный признак Коши и рассуждая аналогичным образом, получим, что можно задать область сходимости степенного ряда как множество решений неравенства при условии существования этого предела, и, соответствен-но, найти еще одну формулу для радиуса сходимости:

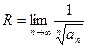(5.4)

- формула Коши-Адамара.