Интегральный признак Коши

Теорема 2.1. Если функция f неотрицательна и убывает на полупрямой х ≥ 1, то ряд сходится или расходится одновременно с несобственным интегралом .

Доказательство.

у Выберем натуральное число k и рассмот-

рим значения х на отрезке k ≤ x ≤ k + 1.

y=f(x) Тогда в силу убывания функции f

f(k) ≥ f(x) ≥ f(k + 1). Проинтегрировав

это неравенство по отрезку единичной

длины [ k, k + 1], получим:

O 1 k k+ 1 x откуда 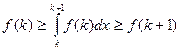. Складывая подобные неравенства, полученные при значениях k от 1 до п, приходим к неравенству: откуда , (2.1)

где . Если ряд сходится и сумма его равна s, то s_n ≤ s, следовательно, , поэтому сходится (см. лемму из лекции №15 2-го семестра).

Если же, наоборот, предположить, что сходится , то из (2.1) следует, что

.

Значит, последовательность частичных сумм ряда ограничена сверху и возрастает, следовательно, по теореме 1.6 ряд сходится.

Пример. Применим интегральный признак Коши к исследованию сходимости рядов вида , сравнивая их с интегралами Рассмотрим следующие возможные значения α:

а) α > 1. Тогда (так как при α > 1

). Следовательно, несобственный интеграл сходится, а значит, сходится и рассматриваемый ряд.

б) α = 1. При этом - интеграл расходится, поэтому расходится и ряд.

в) α < 1. Тогда (так как при α < 1

). Из расходимости несобственного интеграла следует расходимость исследуемого ряда.

Замечание. Итак, ряд вида сходится при α > 1 и расходится при α ≤ 1. Это свойство ряда будет часто использоваться в дальнейшем.