Тригонометрическая форма комплексного числа

Каждому комплексному числу можно сопоставить точку на плоскости. Эта точка будет иметь координаты .

y

Im z

z = x + i y

·

·

y

0 00 O

x

x

Re z

Рис.1.1

Соединим начало координат с точкой z. Расстояние от начала координат до точки z называется модулем комплексного числа z и обозначается . Угол (рис.1.1) называется аргументом комплексного числа и обозначается . Если , тогда называют главным значением аргумента. Все множество аргументов опишется соотношением

,

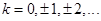
Нетрудно видеть: ,

Заметим: а) ,

б) , 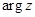не определен,

в) , .

Используя равенства , , комплексное число z можно записать в виде

(1.7)

Такое выражение называется тригонометрической формой комплексного числа.