Упражнения к Глава 2

2.1. Выпишите первые пять членов последовательностей, заданных формулами: ; ; ; .

2.2. Выпишите первые пять членов последовательности, составленной из десятичных приближений по избытку для числа .

2.3. Найдите хотя бы одну формулу общего члена для следующих последовательностей:
;
;
;
;

2.4. Последовательность задана рекуррентным соотношением: . Известно, что . Выпишите первые десять членов этой последовательности.

2.5. Докажите, что последовательность с общим членом монотонно убывает, а с общим членом - монотонно возрастает.

2.6. Пусть - периметр правильного -угольника, вписанного в окружность радиуса . Докажите, что последовательность монотонно возрастает.

2.7. Монотонны ли последовательности, заданные формулами: ; ; ?

2.8. Последовательность задана рекуррентным соотношением: , причем . Докажите, что эта последовательность монотонно убывает.

2.9. Последовательность задана рекуррентным соотношением: , причем . Докажите, что эта последовательность монотонно возрастает.

2.10. Докажите ограниченность последовательности из предыдущего упражнения.

2.11. Докажите ограниченность последовательностей, общие члены которых заданы формулами: ; ; .

2.12. Даны следующие последовательности:

1) ;	2) ;
3) ;	4) ;
5) ;	6) ;
7) 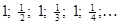;	8) ;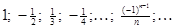
9)

Докажите, что: 0 есть предел последовательностей (1), (2), (8); 1 не является пределом последовательности (1); найдите пределы последовательностей (3), (4), (9); имеют ли пределы последовательности (5), (6), (7)?

2.13. Вычислите пределы:

1) ;	2) ;
3) ;	4) ;
5) ;	6) ;
7) ;	8) ;
9) ;	!0) .

2.14. Используя аксиому Больцано-Вейерштрасса, найдите пределы последовательностей:

1) ;	2) ;
3) ; 4) .

2.15. Докажите, что .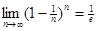

2.16. Вычислите пределы:

1) ;	2) ;
3) .

2.17. Докажите части (3) и (4) ►Теорема 4.

2.18. Вычислите предел:

1) ;	2) ;
3) ;

2.19. Докажите теоремы о пределе частного и о пределе корня, используя бесконечно малые последовательности.

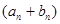2.20. Последовательности и не имеют предела. Могут ли иметь пределы последовательности и 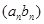? Приведите примеры.

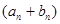2.21. Последовательность имеет предел, а последовательность его не имеет. Могут ли иметь пределы последовательности и ?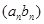

2.22. Пусть 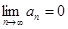, а – произвольна. Можно ли утверждать, что ?

2.23. Известно, что . Можно ли отсюда вывести что: либо , либо ?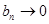

2.24. Пусть последовательности и сходятся к одному и тому же пределу, как ведет себя последовательность ?

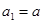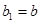
2.25. Последовательности и задаются соотношениями ; ; ; 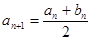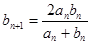. Докажите, что они имеют общий предел, и найдите его.

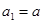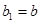
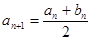2.26. Последовательности и определяются соотношениями ; ; ; . Докажите, что они имеют общий предел.

[1] Понятие функции подробно рассмотрено в Главе 3

[АМ1]Ссылка на?