Сложные проценты

Рассмотрим величину, изменение которой подчинено следующему закону: за одинаковые промежутки времени она изменяется в одно и то же число раз.

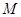Пусть ежегодный прирост особей данного вида животных при условии достаточного количества пищи и неизменных внешних условиях равен . Если в момент времени число особей равно , то через год оно станет равным 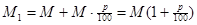. Ещё через год окажется особей и так далее. Вообще, число особей данного вида через лет будет выражаться формулой: .

Эта формула называется формулой сложных процентов. По ней изменяется не только количество особей данного вида, но и, к примеру, количество денег, лежащих в банке.

Рассмотрим, что произойдет, если взять закон увеличения: за года. Тогда через один год число особей (или денег в банке) окажется равным: .

Понятно, что с увеличением выражение возрастает, но неясно, возрастает ли оно неограниченно или имеет какой-то предел. Для выяснения ответа на этот вопрос рассмотрим поведение последовательности при . Для простоты будем считать, что , тогда - последовательность, сходимость которой будем исследовать.

21. Число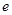

Рассмотрим не только последовательность , но и , . Так как и 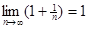, то из сходимости последовательности 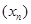вытекает, что последовательность сходится к тому же самому пределу.

Докажем, что последовательност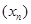и и возрастают, а - убывает.

Воспользуемся неравенством Коши для набора из числа, в котором чисел равны 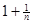, а последнее число – единица: .

Их среднее арифметическое , а среднее геометрическое , , значит, , откуда , то есть для всех .

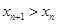Аналогично доказывается, что возрастает последовательность (докажите это самостоятельно, используя набор чисел: ).

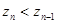Итак, имеем , значит, , , но тогда , значит, , то есть для всех и последовательность убывает.

Для любого натурального имеем: , но , .

Итак, последовательность 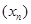возрастает и ограничена сверху, значит, последовательность 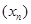- сходящаяся (по аксиоме Больцано-Вейерштрасса). Обозначим её предел 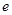(в честь Леонарда Эйлера), итак, - один из замечательных пределов.

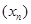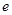Последовательности и стремятся к числу с разных сторон: 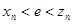, поэтому с их помощью можно получить (хоть и довольно медленно) число 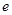с любой степенью точности.

Вот несколько первых десятичных знаков числа Это число иррационально и трансцендентно.

22. Вычисление пределов, связанных с числом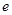

Вычисление пределов многих последовательностей связано с числом 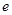. При этом мы используем следующее утверждение, которое оставляем без доказательства:

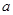►Теорема 7. Если , и хотя бы одно из чисел и 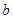отлично от нуля, то .

Пример 37. Вычислить .

Перепишем заданную последовательность так: .

Числа образуют подпоследовательность последовательности натуральных чисел, поэтому из того, что следует, что ; кроме того, , значит, .