Свойства сходящихся последовательностей

►Теорема 1. Если последовательность сходится, то она имеет только один предел.

Доказательство: пусть и , где ,тогда для любого положительного числа найдется натуральное число такое, что для и найдется такое натуральное число , что для .

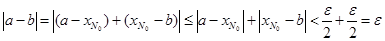Возьмем , тогда имеем: и , следовательно . , но - любое сколь угодно малое положительное число Значит, . Полученное противоречие доказывает теорему.

►Теорема 2. Если последовательность сходится, то она ограничена.

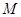Доказательство: пусть , тогда и . Если в качестве выбрать 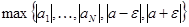, то .Обратное утверждение неверно, например . Эта последовательность ограничена, но не имеет предела.

►Теорема 3. («о двух милиционерах»). Пусть даны три последовательности , и , причем последовательности и имеют один и тот же предел: и пусть для всех натуральных выполняется неравенство: 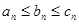. Тогда последовательность сходится, причем её предел равен .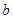

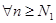
Доказательство: пусть произвольное сколь угодно малое число, тогда () ; () 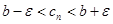; пусть , тогда выполняются неравенства: 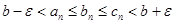или .

Итак, , значит, .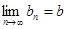

Пример 33. Найти .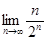

Решение: применить теорему о пределе частного нельзя, так как не существует предела ни числителя, ни знаменателя. Воспользуемся теоремой «о двух милиционерах», предварительно доказав неравенство: (*) для всех .

Действительно, при неравенство (*) выполнено: ; пусть при , где , верно неравенство ; докажем, что верным будет и неравенство . Тогда, на основании принципа математической индукции, неравенство (*) будет верно для всех .

Рассмотрим , так как при . Итак, верно , значит, и для всех .

Известно, что и , значит, 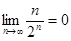(по теореме «о двух милиционерах»).

►Теорема 4. Если последовательност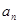и и сходятся, то:

1) ,

2) ,

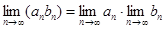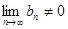3) Если, кроме того, для любого и , то .

4) .

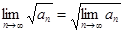Доказательство: докажем часть (1) ►Теорема 4:

Нам нужно проверить, что , где , .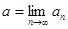

Так как , то .

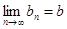Так как , то .

Пусть , тогда , а это означает, что , где , .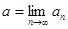

Докажем часть (2) ►Теорема 4:

Рассмотрим , последовательность 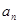имеет предел, значит, она ограничена, то есть .

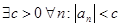Так как , то .

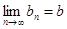Так как , то .

Возьмем , тогда при имеем .

Итак, 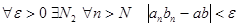, то есть .

Части (3) и (4) доказываются аналогично.