Ограниченность числовых последовательностей

Определение 27. Последовательность называется ограниченной, если существует положительное число 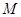такое, что для всех членов последовательности выполняется неравенство .

Краткая запись (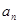 ограничена) .

Последовательность ограничена, так как .

Последовательность ограничена, так как .

Не всякая последовательность является ограниченной.

Пример 31. Докажите, что последовательность не является ограниченной.

Доказательство: предположим, что последовательность ограничена, это означает, что 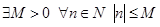. Однако, например, для это неравенство не выполняется. Следовательно, предположение неверно, и не является ограниченной.

Определение 28. Последовательность, не являющаяся ограниченной, называется неограниченной.

Сформулируем равносильное этому позитивное определение неограниченной последовательности.

Определение 29. Последовательность 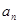неограниченная, если для любого числа 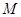найдется такой номер , что .

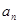( неограниченная) .

Если изображать члены последовательности точками на координатной прямой, то все члены ограниченной последовательности лежат на некотором отрезке.

Для неограниченной последовательности вне любого отрезка найдутся члены этой последовательности.