Основные определения. Рассмотрим последовательность и вычислим несколько её первых членов: ; ;

Рассмотрим последовательность и вычислим несколько её первых членов: ; ; ; ; ;…; ;…

Мы видим, что члены последовательности, возрастая, стремятся к числу 2. Разность становится тем меньше, чем больше . Действительно, все члены, начиная с одиннадцатого, отличаются от числа 2 меньше, чем на 0,1; а все члены, начиная со 101-го, отличаются от числа 2 меньше, чем на 0,01 и так далее.

В таком случае говорят, что последовательность имеет предел, равный числу 2.

Дадим строгое определение предела числовой последовательности.

Определение 30. Число называется пределом последовательности 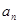, если для любого положительного числа (греческая буква «эпсилон») найдется такое натуральное число 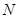, что для всех номеров , бóльших 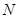, выполняется неравенство . В этом случае пишут .

С помощью кванторов определение можно записать следующим образом: .

Заметим, что неравенство равносильно неравенствам или . Это означает, что число 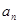принадлежит интервалу .

Определение 31.

Рисунок 9

Интервал называется –окрестностью точки .

Рассмотрим геометрический смысл определения предела последовательности.

Определение 32.

Рисунок 10

Число называется пределом последовательности 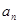, если в любую –окрестность числа попадают все члены последовательности, кроме, быть может, конечного числа их.

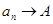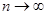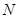Действительно, если при , то для каждого найдется такое , что все члены последовательности с номерами лежат в –окрестности числа и, значит, вне этой окрестности могут находиться только первые 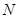членов последовательности.

Пример 32. Докажем, что .

Доказательство: для любого внутрь интервала попадут все члены последовательности, которые удовлетворяют неравенству . (*)

Решая это неравенство, находим, что .

Следовательно, все члены последовательности, номер которых , удовлетворяют неравенству (*). Если в качестве N взять число , то .

Не всякая последовательность имеет предел. Рассмотрим, например, последовательность . Очевидно, члены последовательности принимают значение или . Эта последовательность не имеет предела. Действительно, если взять -окрестности и , то в них находится бесконечно много членов последовательности, но и вне каждой окрестности – также бесконечно много.

Определение 33. Последовательность, имеющая предел, называется сходящейся, а последовательность, не имеющая предела, расходящейся.