Предельные теоремы

Предельные теоремы – это собирательное название для целого класса теорем, описывающих закономерности, которые возникают в результате суммарного действия случайных величин. В этом классе можно выделить две группы.

Теоремы первой группы называют законом больших чисел. Примером действия этого закона служит сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний.

Теорема Бернулли: Если в каждом из n независимых испытаний вероятность Р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности Р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.n

Иначе, если e – сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство:

.[6]

Позднее были получены различные обобщения этой теоремы.

Теоремы второй группы устанавливают условия, при которых совокупное действие случайных величин приводит к нормальному закону распределения. На практике часто используются локальная и интегральная теоремы Муавра-Лапласа, дающие асимптотические формулы для вычисления вероятностей в случае схемы испытаний Бернулли (см. Биномиальное распределение).

Формула Бернулли позволяет вычислить вероятность того, что событие появится в n испытаниях ровно k раз. Однако при больших значениях n вычисления становятся настолько громоздкими, что применение формулы становится весьма затруднительным. Обойти эти затруднения позволяет локальная теорема Муавра-Лапласа, дающая асимптотическую формулу для приближенного нахождения вероятности появления события ровно k раз в n испытаниях, если число испытаний n достаточно велико. (Заметим, что в отличие от формулы Пуассона эта теорема не требует выполнения условия np=const).

Локальная теорема Лапласа (Муавра-Лапласа): Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна

,

где , q=1-p. n

Для положительных х имеются таблицы значений функции . Для отрицательных х используют те же таблицы, поскольку функция j(х) четная.

Предположим, что имеют место условия предыдущей теоремы. Вычислить вероятность P_n(k₁, k₂) того, что событие А произойдет в n испытаниях не менее k₁ раз и не более k₂ раз помогает интегральная теорема Муавра–Лапласа.

Интегральная теорема Муавра – Лапласа: Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k₁, k₂) того, что событие А появится в n испытаниях не менее k₁ раз и не более k₂ раз, приближенно равна

, где , .n

На практике для вычисления искомой вероятности используют таблицы функции Лапласа 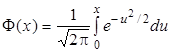. При этом P_n(k₁, k₂) удобно представить как .

Следствие: Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний имеет место следующее:

А) вероятность того, что число m наступлений события A отличается от произведения np не более, чем на величину (по абсолютной величине), можно оценить как

Б) вероятность того, что относительная частота события A заключена в пределах от a до b можно оценить как

,

где , .

Пример 5.14.

В 25 пачках печенья из 400 были обнаружены призовые купоны. На сколько призовых купонов в 1000 пачек можно рассчитывать с вероятностью 0,95?