Математична модель задачі лінійного програмування

Ми будемо розглядати задачі пошуку екстремуму (мінімуму або максимуму), лінійної функції за умов, які є лінійними нерівностями або рівняннями, інакше кажучи, лінійні оптимізаційні задачі. Загальні методи розв’язання таких задач вивчаються дисципліною, яка зветься лінійне програмування (ЛП), а самі задачі — задачами лінійного програмування (ЗЛП). ЛП є, у свою чергу, підрозділом іншої дисципліни, що має назву математичне програмування.

Методику розв’язання ЗЛП малих розмірностей ми розглянемо на прикладі двовимірної ЗЛП:

4.1.1. Задача планування виробництва в умовах обмежених ресурсів.

Деяка фірма випускає пилососи і вентилятори. Серед матеріалів, потрібних для виготовлення виробів, “критичними” є мідний дріт і трансформаторне залізо (“критичні” - означає, що саме ці матеріали знаходяться в обмеженій кількості і саме вони визначають обсяг продукції). Для виготовлення одного пилососа потрібно 0,6 кг мідного дроту і 0.3 кг трансформаторного заліза, одного вентилятора - 0,3 кг мідного дроту і 0,2 кг трансформаторного заліза. В наявності є 48 кг мідного дроту і 30 кг трансформаторного заліза. Чистий прибуток від реалізації одного пилососа складає 120, а одного вентилятора – 70 умовних грошових одиниць. Треба визначити план випуску пилососів і вентиляторів (кількість пилососів і вентиляторів, яку потрібно виробити) для якого вистачило б запасів дроту і заліза і якому відповідав би максимальний прибуток.

4.1.2. Формалізація задачі планування виробництва в умовах обмежених ресурсів.

Вводимо змінні: - кількість пилососів, 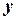- кількість вентиляторів. Тоді потрібна кількість дроту та заліза буде такою:

	дріт	залізо
х - кількість пилососів у - кількість вентиляторів	0,6× х 0,3× у	0,3× х 0,2× у

(для одного потрібно 0,6 кг, а для х =0,6× х).

Сумарна кількість дроту та заліза не повинна перевищувати їх запасів. Звідси отримуємо умови:

.

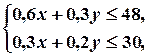
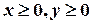Цільова функція задачі - це функція прибутку від реалізації х пилососів і у вентиляторів. Цю функцію ми назвемо :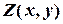

.

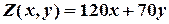Прибуток (функцію 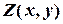) ми хочемо максимізувати; отже маємо задачу пошуку екстремуму, а саме, максимуму (max), лінійної функції за умов, які є лінійними нерівностями, тобто лінійну оптимізаційну задачу.

4.1.3. Загальна структура задачі лінійного програмування.

Математична модель задачі ”Планування виробництва” має вигляд:

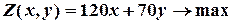(цільова функція)

(прямі обмеження - умова невід’ємності змінних)

(непрямі обмеження)