Властивості векторного добутку

Важлива геометрична властивість векторного добутку “закладена” у його означення: якщо вектори 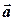і 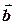зведені до спільного початку, то модуль векторного добутку дорівнює площі паралелограма, побудованого на векторах 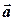і .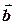

Друга важлива геометрична властивість випливає із зазначеної і подається теоремою:

Теорема (критерій колінеарності двох векторів). Векторний добуток двох векторів рівний нуль-вектору тоді і тільки тоді, коли ці вектори колінеарні.

Доведення необхідності. Треба довести, що якщо векторний добуток векторів 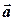і 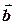дорівнює нулю, то (з необхідністю) вектори 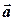і 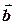колінеарні.

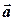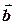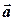Нехай , тоді , а отже й . Якщо ж жоден з векторів і не рівний нуль-вектору, то з попереднього рівняння отримаємо , отже вектори і 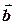колінеарні. Якщо хоча би один з векторів 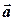і 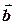дорівнює нуль-вектору, то ми можемо вважати його колінеарним іншому, так як нульовий вектор можна вважати напрямленим будь-як.

Доведення достатності. Треба довести, що якщо вектори 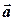і 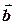колінеарні, то цього достатньо, щоб їх векторний добуток дорівнював нулю.

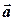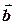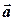Нехай вектори і колінеарні, тоді кут між ними або дорівнює 0 (у випадку коли і 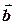напрямлені в одну сторону), або дорівнює 180⁰ (у випадку, коли 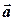і 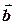напрямлені в протилежні сторони). І в тому, і в іншому випадку . З цього випливає, що , тобто модуль вектора рівний нулю, а це означає, що сам вектор дорівнює нуль-вектору.