Теорема косинусів. В

Доведення. Нехай у трикутника маємо:

Вектор

Якщо , cos — додатний, то , то .

Якщо - гострий, то .

Якщо - тупий, соs <0, то , - гострий.

3.5.2.4.Геометричний образ лінійної нерівності.

Лінійне рівняння з двома змінними визначає пряму лінію на координатній площині (з трьома змінними — — площину в просторі). Нехай 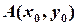— деяка точка на цій прямій лінії, тоді можна загальне рівняння перетворити до вигляду:

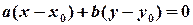
Це рівняння виражає таку умову:

Умова: точка 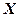належить прямій 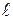тоді і тільки тоді, коли вектор .

Ліва частина останнього рівняння є скалярний добуток саме вказаних векторів ( і ).

З означення скалярного добутку () випливає, що нерівність задовольняють ті і тільки ті точки площини, радіус-вектор яких від точки А, що належить прямій 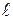утворює з нормальним вектором гострий кут .

Точка задовольняє нерівність , коли радіус-вектор утворює гострий кут з нормальним вектором . Отже, множиною розв’язків лінійної нерівності - є півплощина -1.

Аналогічно, множиною розвязків нерівності є протилежна півплощина -2.

Приклад.

Для визначення того, яку саме півплощину визначає нерівність, можна скористатися способом пробних точок. Беремо будь-яку точку, і якщо вона задовольняє нерівність, то саме цю півплощину визначає нерівність, якщо не задовольняє, — то іншу (протилежну) півплощину:

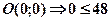
це правильна нерівність, отже, нерівність 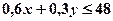визначає ту півплощину, у якій знаходиться точка .

Якщо ми розглядаємо систему з кількох нерівностей, то множиною розв’язків цієї системи є перетин відповідних півплощин, тобто це є така множина точок, які потрапляють в кожну з півплощин: