Схема исследования и построения графика функции

Чтобы исследовать функцию y=f (x) и построить ее график, действия рекомендуется проводить в следующем порядке.

1. Нахождение области определения функции. Исследование на четность, нечетность, периодичность. Нахождение точек пересечения графика с осями координат.

2. Исследование функции на непрерывность. Вычисление пределов функции при , стремящемся к границам области определения и к точкам разрыва.

3. Нахождение асимптот функции.

4. Вычисление f ' (x) и исследование ее знаков. Нахождение интервалов возрастания, убывания и экстремумов.

5. Вычисление f ''(x) и исследование ее знаков. Нахождение интервалов направления выпуклости и точек перегиба.

6. Построение таблицы, в которой указываются все найденные точки разрыва, критические точки первого и второго порядка и интервалы между ними. В каждом интервале характеризуется поведение функции.

7. Построение графика функции с учетом ее асимптот и таблицы. При необходимости можно вычислить промежуточные значения функции.

Пример. Исследовать функцию и построить ее график.

1. Функция определена в области D=(-¥,0) È (0, ¥). С осями координат график не пересекается, так как при х=0 она не определена и f(x)>0"xÎD. Функция не является четной, нечетной и периодичной.

2. Функция непрерывна в своей области определения, х₀ = 0 – ее точка разрыва.

Следовательно, прямая х = 0 – вертикальная асимптота

3. , . Поэтому прямая y==1 является правой и левой наклонной асимптотой функции.

4.
Знаки этой производной следующие (рис.11).

Рис. 11

Поэтому на промежутках (-¥,0) и (0,¥) функция убывает.

Критических точек и экстремумов нет.

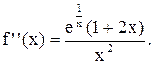Знаки f ''(x) (рис.12)

o

В промежутке функция выпукла вверх, в промежутках , она выпукла вниз. Критическая точка второго порядка является точкой перегиба функции.

6.

X	(-¥,- )	-	(- ,0)		(0, +¥)
f '(x)	¾	¾	¾	не $	¾
f ''(x)	¾		+	не $	+
f (x)				не $

точка точка
перегиба разрыва 2-го рода

8. Построение графика начинаем с асимптот и критических точек, затем пользуемся таблицей (рис.13).

Контрольные вопросы:

1.Сформулируйте определение точки экстремума функции. Два правила для отыскания экстремумов функции.

2. Нахождение экстремума функции с помощью первой производной

3. Нахождение экстремума функции с помощью второй производной

4. Нахождение точки перегиба функции

5. Формула нахождения асимптоты графика функции

6. Изложите схему общего исследования функции и построения ее графика.

7. Эволюта и эвольвента плоской кривой

8. Кривизна кривой

Литература:

[2] Глава 4, § 4.17-4.23 стр. 178-203

[19] 3.7 стр. 209-219