 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные теоремы дифференциального исчисления и их приложения
|
|
Определение. Дифференциалом 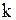 –го порядка называется дифференциал от ее дифференциала
–го порядка называется дифференциал от ее дифференциала 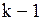 –го порядка
–го порядка
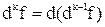 ,
,
вычисленный в предположении, что 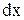 остается постоянной.
остается постоянной.
Получаем формулы для вычисления такого дифференциала:
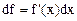 ,
,
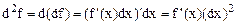 ,
,
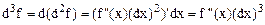 ,
,
… … … … … … … … … … … … … … …
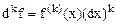 .
.
Из последней формулы имеем еще одно обозначение для производной 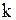 –го порядка.
–го порядка.
Для дифференциалов 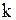 –го порядка также справедливы следующие правила:
–го порядка также справедливы следующие правила:
1) 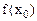 ,
, 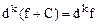 .
.
2) 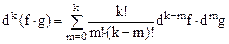 ,
, 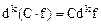 .
.
Определение. Точка 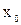 называется точкой минимума (максимума) функции,
называется точкой минимума (максимума) функции,  , если она определена в некоторой окрестности
, если она определена в некоторой окрестности 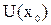 этой точки и для
этой точки и для 
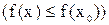 .
.
Значение 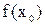 в этом случае называется минимумом (максимумом) функции. Точки минимума и максимума называются экстремальными точками, а соответствующие значения функции–экстремумами.
в этом случае называется минимумом (максимумом) функции. Точки минимума и максимума называются экстремальными точками, а соответствующие значения функции–экстремумами.
Функция, определенная на отрезке 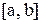 , имеет там только одно наибольшее и наименьшее значения, но может иметь несколько максимумов и минимумов. При этом некоторые максимумы могут быть меньше минимумов (рис.2).
, имеет там только одно наибольшее и наименьшее значения, но может иметь несколько максимумов и минимумов. При этом некоторые максимумы могут быть меньше минимумов (рис.2).
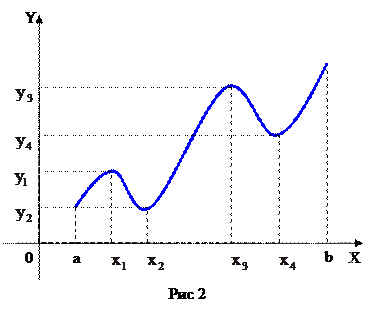
Здесь 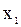 и
и 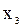 – точки максимумов,
– точки максимумов, 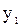 и
и 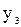 – максимумы;
– максимумы; 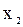 и
и 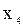 – точки минимумов;
– точки минимумов; 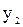 и
и 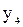 – минимумы;
– минимумы;  – экстремальные точки,
– экстремальные точки, 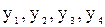 – экстремумы.
– экстремумы.
Теорема Ферма. Пусть 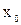 – точка минимума, т.е.
– точка минимума, т.е. 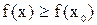 для
для 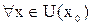 .
.
Тогда для 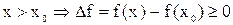 ,
, 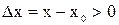 и
и
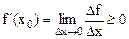 .
.
Для 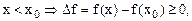
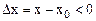 и
и
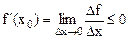 .
.
Следовательно, 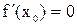 .
.
Заметим, что если 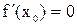 , то касательная к графику функции
, то касательная к графику функции  в этой точке параллельна оси
в этой точке параллельна оси 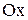 (так как тангенс угла наклона этой касательной равен нулю). Поэтому геометрический смысл теоремы Ферма состоит в том, что касательная в экстремальной точке функции (если она существует) параллельна оси
(так как тангенс угла наклона этой касательной равен нулю). Поэтому геометрический смысл теоремы Ферма состоит в том, что касательная в экстремальной точке функции (если она существует) параллельна оси 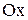 (рис3).
(рис3).
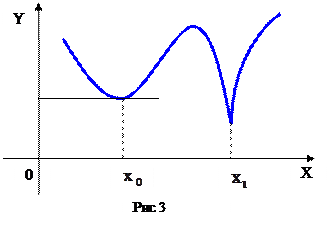
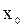 и
и 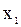 – точки минимума, в
– точки минимума, в 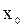 – касательная параллельна оси
– касательная параллельна оси 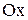 , в точке
, в точке 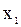 касательной нет.
касательной нет.
Следующие три теоремы выявляют свойства функций, дифференцируемых на отрезке.
Определение. Функция  называется дифференцируемой на отрезке
называется дифференцируемой на отрезке 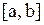 , если она непрерывна на этом отрезке и имеет производную во всех точках интервала
, если она непрерывна на этом отрезке и имеет производную во всех точках интервала 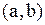 .
.
Для таких функций кроме теорем Больцано–Коши и Вейерштрасса справедливы еще следующие теоремы.
Теорема Ролля. Пусть функция  дифференцируема на отрезке
дифференцируема на отрезке 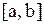 и принимает на его концах равные значения:
и принимает на его концах равные значения: 
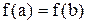 . Тогда
. Тогда 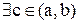 такая, что
такая, что  .
.
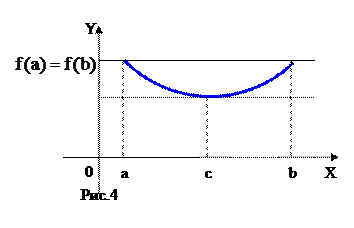
Геометрический смысл этой теоремы состоит в том, что при выполнении ее условий 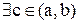 , в которой касательная к графику функций параллельна оси
, в которой касательная к графику функций параллельна оси 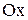 и хорде, соединяющей концы графика на отрезке
и хорде, соединяющей концы графика на отрезке 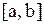 (рис.4).
(рис.4).
 |
Пример. В интервале (–1,1) нет точек, в которых касательная к графику 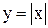 параллельна оси
параллельна оси 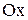 . Здесь нарушается условие теоремы Ролля: в точке
. Здесь нарушается условие теоремы Ролля: в точке 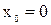 функция
функция 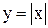 не дифференцируема, хотя
не дифференцируема, хотя 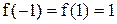 .
.
Теорема Коши. Пусть функция  и
и 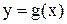 дифференцируемы на
дифференцируемы на 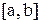 и
и 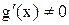 для
для 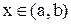 . Тогда
. Тогда 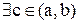 такая, что
такая, что
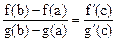 .
.
Следующая теорема является прямым следствием теоремы Коши, однако, в силу ее широкого применения имеет специальное название.
Теорема Лагранжа. Пусть функция  дифференцируема на
дифференцируема на 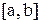 . Тогда в интервале
. Тогда в интервале 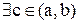 :
:
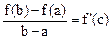 .
.
Заметим, что 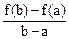
равна тангенсу угла наклона хорды, соединяющей концы графика  на
на 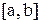 , а
, а 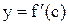 равна тангенсу угла наклона касательной к графику функции в точке
равна тангенсу угла наклона касательной к графику функции в точке 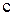 (рис.5).
(рис.5).
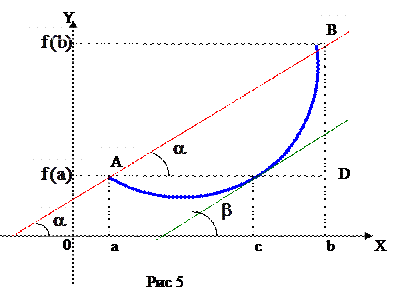
Из равенства этих углов получаем геометрический смысл теоремы Лагранжа. При выполнении условий этой теоремы 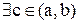 , в которой касательная к графику параллельна хорде, соединяющей концы графика.
, в которой касательная к графику параллельна хорде, соединяющей концы графика.

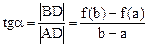 ,
, 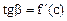 .
.
Следствие 1. Возьмем 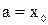 ,
, 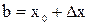 , тогда при выполнении условий теоремы Лагранжа в отрезке
, тогда при выполнении условий теоремы Лагранжа в отрезке 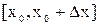 будем иметь
будем иметь
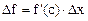 , где
, где 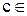
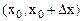 .
.
Это 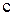 можно записать в виде
можно записать в виде
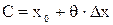 , где
, где 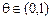 .
.
Тогда приращение функции записывается в виде

или в общем виде 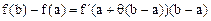 .
.
Следствие 2. Пусть функция  дифференцируема и
дифференцируема и 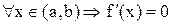 , тогда эта функция постоянна в
, тогда эта функция постоянна в  , т. е.
, т. е. 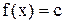 .
.
Контрольные вопросы:
1.Сформулируйте определения производной и дифференциала высших порядков.
2. Инвариантность формы первого дифференциала
3. Формула приближенного вычисления значения функции
4. Правило нахождение производных высшего порядка. Примеры
5. Теоремы Ролля, и ее геометрический смысл
6. Теорема Лагранжа и ее геометрический смысл
Литература:
[2] Глава 4 § 4.1-4.8 стр. 151-178; [19] 3.3-3.6 стр. 191-209; [18] §10.1-10.4 стр. 265-273; [20] §10.1-10.4 стр. 184-192
Тема лекции: Раскрытие неопределенности. Исследование поведения функции и их графиков (2 часа)
Дата публикования: 2014-10-23; Прочитано: 1081 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
