Дифференцирование сложной функции

Пусть функция 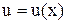дифференцируема в точке 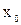, , 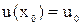функция 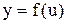дифференцируема в точке 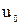, тогда сложная функция 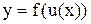дифференцируема в 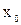и её производная равна .

Примеры:

1. Вычислить .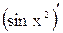

Запишем, , где 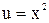. Поэтому

.

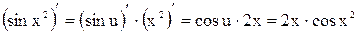2. .

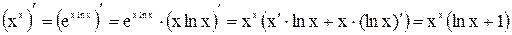Гиперболические функции и их производные: Гиперболический синус 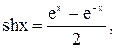область определения D=R, область значений E=R (рис.4).

Y

0 X

Рис. 4

Гиперболический косинус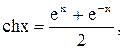

область определений D=R, область значений 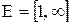(рис.5).

0 X

Рис.5

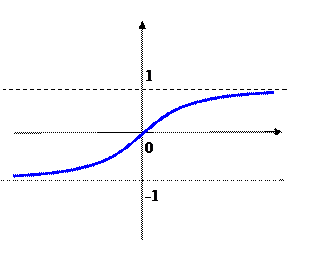Гиперболический тангенс 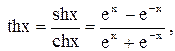область определения D=R, область значений E=(-1,1) (рис.).

Y

X

Рис.6

Гиперболический котангенс 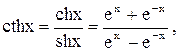область определения 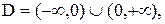область значений 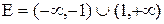(рис).

-

Рис.7

Соотношения, связывающие эти функции, подобны аналогичным соотношениям для тригонометрических функций, например:

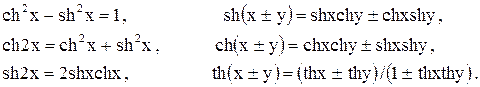
Вычислим производные этих функций, используя правила вычисления производных

.

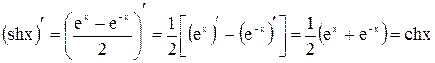Самостоятельно проверьте, что

.

7.3. Обратная функция и её производная

Пусть функция имеет область определения 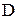и область значений .

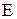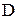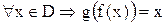Определение. Функция с областью определения E и областью значений называется обратной функции , если для и для .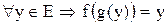

В системе координат Оxy функции и имеют один и тот же график. Функции и 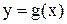имеют графики, симметричные относительно прямой .

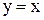Примерами взаимно обратных функций являются функции:

1) 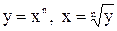, где D=E=R для нечетного n, и 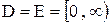для четного n.

2) 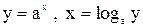, где .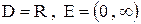

3) .

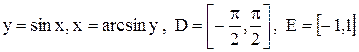4) .

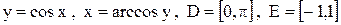5) .

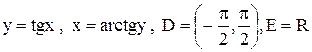Теорема. Если функция 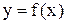непрерывна в промежутке (a,b)(или 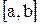), то для того, чтобы у неё существовала обратная, необходимо и достаточно, чтобы была строго монотонна в (a,b), т.е. 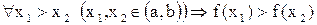или .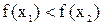

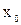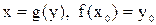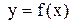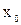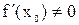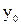Теорема. Пусть функция непрерывна в окрестности и имеет в ней обратную функцию . Тогда, если дифференцируема в точке и , то дифференцируема в точке и

.

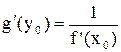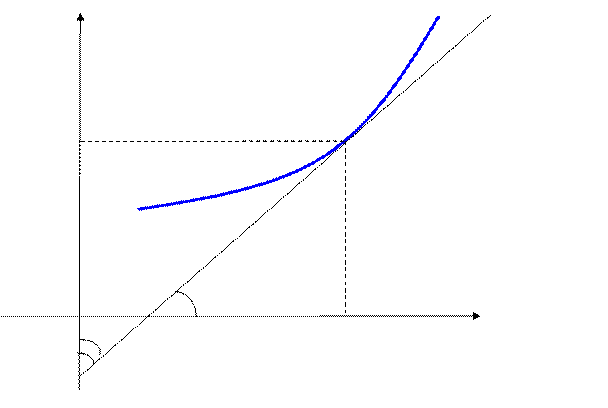
Геометрический смысл этой теоремы состоит в том, что тангенсы углов наклона касательной к графику (или ) к осям Оx и Оy взаимно обратны (рис.8).

Y

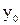
0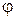

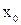X

Рис. 8

.

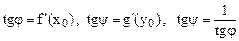Пример

1. .

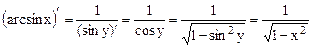Здесь . Для .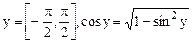

Проверьте, что .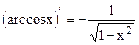

2. .

Таблица производных основных элементарных функций

Эту таблицу необходимо знать наизусть.

Таблица

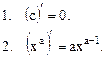
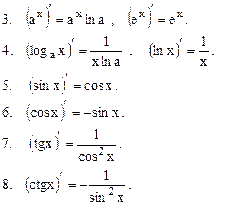
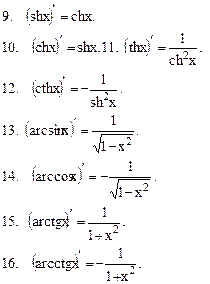
С помощью этой таблицы и правил вычисления производных можно вычислить производную любой элементарной функции.