Для этого определим интервалы знакопостоянства ее производной

.

Этот квадратный трехчлен имеет корни x₁=0, x₂=2, поэтому при и в этом промежутке функция y = x³ – 3x² + 1 строго убывает.

При , f ' (x)>0 и в этих промежутках функция строго возрастает. Так как f(0)=1 и f(+2)= - 3, то эскиз графика функции имеет вид (рис.1).

Вспомните теперь определение экстремальных точек функции.

Определение. Точка x₀, в которой f(x₀) непрерывна, а производная функции y=f(x) равна нулю или не существует, называется критической точкой этой функции.

Теорема (необходимое условие экстремума). Пусть x₀ – экстремальная точка функции y=f(x), тогда x₀ – критическая точка этой функции.

Пример. Функция y = x³ имеет критическую точку x₀=0, так как это единственное решение уравнения f ' (x)=3 x ²=0.

Однако экстремальных точек у этой функции нет, y=x³ строго возрастает на всей числовой оси.

Теорема (достаточное условие экстремума). Пусть функция y=f(x) непрерывна в окрестности U(x₀) критической точки x₀ и дифференцируема в U(x₀) кроме быть может самой точке x₀. Тогда

1) если в U(x₀) f ' (x)>0 при х<x₀ и f '(x)<0 при x>x₀, то x₀ ¾ точка максимума;

2) если в U(x₀) f ' (x)<0 при х<x₀ и f '(x)>0 при x>x₀, то x₀ ¾ точка минимума;

3) если в U(x₀) f ' (x)>0 или f '(x)<0 при x¹ x₀, то в x₀ ¾ экстремума нет.

Итак, чтобы определить экстремальные точки функции необходимо найти все ее критические точки и установить знаки производной в интервалах между ними. Затем согласно достаточному условию экстремума исследуются найденные критические точки. Точки непрерывности функции, где производная меняет свой знак с "плюса" на "минус", являются точками максимума; точки, где производная меняет свой знак с "минуса" на "плюс", являются точками минимума; точки, где производная свой знак не меняет, экстремальными не являются.

Пример. Исследовать функцию на возрастание, убывание и экстремумы.

Производная функции не существует при x₁=0.

Из уравнения получаем вторую критическую точку . Методом интервалов определяем знаки f ' (x) (рис.2).

Функция всюду непрерывна; согласно достаточному условию экстремума x₁=0 есть точка максимума, а точка минимума. В интервалах (–¥, 0) и эта функция возрастает, а в интервале она убывает. Результаты исследования занесем в таблицу

x	(–¥,0)		(0, )		(, +¥)
f '(x)	+	не $	–		+
f (x)		max		min

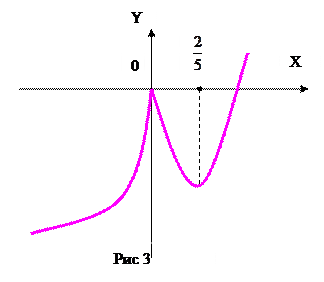Построим теперь эскиз графика функции, учитывая, что при х®0
f '(x) является бесконечно большой (рис.3).

Приведем еще один достаточный признак экстремума, использующий вторую производную функции.

Теорема. Пусть функция y=f(x) дифференцируема в некоторой окрестности критической точки х₀ и f ''(x₀) существует. Тогда, если
f ''(x₀)>0, то x₀ - точка минимума, а если f ''(x₀)<0, то x₀ - точка максимума.

Пример. Найти экстремальные точки функции y=2sinx+cos2x.

В силу ее периодичности достаточно рассмотреть отрезок [0,2 ]. Найдем критические точки из уравнения

f ' (x)=2cosx–2sin2x=0Þ cosx– 2sinxcosx = 0 Þ cosx(1 – 2sinx)=0.

Из уравнения cosx=0 получаем , , а из уравнения
1 – 2sinx=0 Þ , .

Вычислим f '' (x)=–2sinx–4cos2x.

, , , .

Итак, точки , являются точками минимума, а , 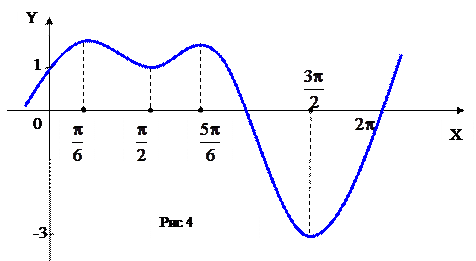точками максимума (kÎ Z). График этой функции имеет вид (рис.4).

С помощью исследования экстремумов можно находить наибольшее и наименьшее значение функции на отрезке. Поскольку 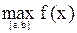может достигаться или на концах отрезка [a,b] или в одной из точек максимума, то для его нахождения необходимо найти все максимумы функции в [a,b],
f(a), f(b) и затем из этих чисел выбрать наибольшее:

= max{f(a), f(b), f(x_i): x_iÎ(a,b) точки максимумa}.

Аналогично

= min{f(a), f(b), f(x_i): x_iÎ(a,b) точки минимумa}.

Пример Найти и для f(x)=x³–3x+3.

(x)=3x² – 3 существует для всех х. Из уравнения 3х² – 3=0 получаем критические точки х_1,2=±1, х_1,2Î[–2,3], f ''(x)=6x, , х₁=1 – точка минимума.

f '' (–1)= –6<0 Þ x₂= –1 точка максимума. Поэтому

f(-2)=1, f(3)=27-9+3=21, f(-1)=-1+3+3=5, f(1)=1-3+3=1

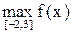= max{f (-2), f (3), f (-1)} = max{1,21,5} = 21.

= min{f (-2), f (3), f (1)} = min{1,21,1} = 1.

Выпуклость и точки перегиба. Пусть функция y=f (x) дифференцируема в (a,b).

Определение. Функция y=f (x) называется выпуклой вниз (вверх) в интервале (a,b), если для любого x₀Î(a,b) значение функции в
"хÎ(a,b) не меньше (не больше) соответствующей ординаты касательной к графику функции, проведенной в точке (x₀, f (x₀)) (рис.5).

Теорема. Пусть функция y=f(x) дважды непрерывно дифференцируема в (a,b). Эта функция выпукла вниз (вверх) на этом интервале тогда и только тогда, когда f ''(x)³0 (f ''(x) 0) "xÎ(a,b).

1) Пусть y = f (x) выпукла вниз на (a,b), тогда y_ф-y_k ³ 0 и f ''(c₁) ³ 0. Перейдем к пределу при х x₀, получаем, в силу непрерывности f ''(x), что

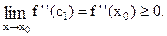
2) Пусть f '' (x) ³0, "xÎ(a,b), тогда получаем, что y_ф–y_k³0, "x₀, хÎ(a,b), т.е. эта функция выпукла вниз.

Аналогично рассмотрите случай функции, выпуклой вверх.

Пример. Гипербола y=1/x в интервале (0, +¥) выпукла вниз, так как 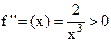, "x₀ (0, +¥), на интервале (–¥, 0) она выпукла вверх, так как , "xÎ (–¥, 0).

Определение. Точка х₀ называется точкой перегиба для функции
y = f (x), если в некоторой окрестности этой точки график функции лежит по разные стороны от касательной к графику, проведенной в точки х₀, т.е. для х>x₀, y_ф-y_k ³ 0, а для х < x₀, y_ф-y_k £ 0 или наоборот. Точку х₀, в которой имеется вертикальная касательная, называют точкой перегиба, если направления выпуклости функции по разные стороны от х₀ противоположны (рис.6).

	а), б)x0-точка перегиба, в)x1-не точка перегиба

Теорема (необходимое условие существования точки перегиба)

Пусть функция y=f(x) дважды непрерывно дифференцируема в U(x₀)\{x₀} и непрерывна в х_0. Тогда → если → → точка → перегиба → то или не существует.

Такие точки х₀, в которых f (x₀) непрерывна, а f "(x₀)=0 или не существует, называются критическими точками второго порядка.

Пример. У функции y=x⁴ точка x₀=0 является критической второго порядка, так как f ''(x)=12x² и f ''(0)=0. Однако эта точка не является точкой перегиба, так как f ''(x)³0 и функция всюду выпукла вниз (лежит выше касательной).

Теорема (достаточное условие существования точки перегиба). Пусть функция y=f (x) дважды непрерывно дифференцируема в U(x₀)\{x₀} и непрерывна в x₀, где x₀ – критическая точка второго порядка. Тогда, если при x<x₀ и x>x₀, f ''(x) имеет разные знаки, то x₀ – точка перегиба этой функции. Если же при x<x₀ и x>x₀, знаки f ''(x) совпадают, x₀ – не точка перегиба.

Итак, чтобы найти точки перегиба функции, необходимо найти все ее критические точки второго порядка и исследовать каждую из них с помощью достаточного условия точки перегиба.

Пример. Найти направление выпуклости и точки перегиба функции

Вычислим

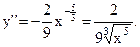
f ''(x) не существует при х₀=0, для остальных х, f ''(x) в нуль не обращается, т.е. х₀=0 – единственная критическая точка второго порядка. Для хÎ(0,+¥), f ''(x)<0, поэтому х₀=0 точка перегиба с вертикальной касательной, так как f '(x) б.б. при х®0. На промежутке (-¥, 0), направлена выпуклостью вниз, а на промежутке (0,+¥) она направлена выпуклостью вверх (рис.7).