 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие дифференциала функции
|
|
Определение. Если приращение функции  в точке
в точке  можно представить в виде
можно представить в виде 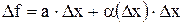 , где
, где 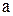 - число, а
- число, а  - б.м. при
- б.м. при  , то величина
, то величина  называется дифференциалом функции
называется дифференциалом функции  в точке
в точке 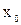 (главной частью приращения).
(главной частью приращения).
Теорема (о дифференциале). Для того, чтобы функция  имела дифференциал в точке
имела дифференциал в точке 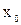 , необходимо и достаточно, чтобы существовала производная
, необходимо и достаточно, чтобы существовала производная 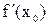 , при этом
, при этом  . (т.е.
. (т.е.  ).
).
Из этой теоремы становится ясным, почему существование производной у функции и существование дифференциала называются одним словом- дифференцируемость.
Пример: Пусть y=ax+b, тогда 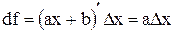 , в частности
, в частности  . Поэтому дифференциал функции
. Поэтому дифференциал функции  обозначают в виде
обозначают в виде 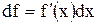 , а её производную записывают как отношение дифференциалов
, а её производную записывают как отношение дифференциалов
 .
.
Выясним геометрический смысл дифференциала. Поскольку  то
то  . Поэтому
. Поэтому  равен приращению координаты касательной, проведённой к графику функции
равен приращению координаты касательной, проведённой к графику функции  в точке
в точке 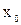 при приращении
при приращении  аргумента
аргумента 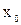 (рис.). Приращение функции |DB| складывается из дифференциала |ВС| и б.м. величины высшего порядка малости по сравнению с
(рис.). Приращение функции |DB| складывается из дифференциала |ВС| и б.м. величины высшего порядка малости по сравнению с 
 . Если в соотношении
. Если в соотношении
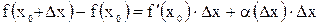 ,
,
пренебречь этой величиной, то получаем формулу для приближенного вычисления значений функции в точке  ,
,  . Y
. Y
 D
D

 C
C

A 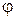
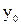 B
B
0 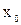
 X
X
Рис 10
Пример. Вычислить приближенно  .
.
Имеем 
 .
.
Правила вычисления дифференциала непосредственно следуют из правил вычисления производных.
Пусть функции  и
и 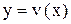 дифференцируемы в точке, тогда
дифференцируемы в точке, тогда
1)  , где с – число.
, где с – число.
2)  .
.
3)  , если
, если 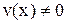 .
.
4) Если функция 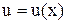 дифференцируема в точке x, а
дифференцируема в точке x, а 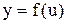 в соответствующей точке u, то для сложной функции
в соответствующей точке u, то для сложной функции  ,
,
 .
.
Это правило называют инвариантностью формы дифференциала. Для функции 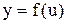 дифференциал
дифференциал  , как в случае, когда u- независимая переменная, так и в случае, когда
, как в случае, когда u- независимая переменная, так и в случае, когда 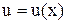 есть функция другой переменной x.
есть функция другой переменной x.
Контрольные вопросы:
1.Сформулируйте определение производной. Каков ее механический и геометрический смысл?
2.Сформулируйте правило логарифмического дифференцирования. Приведите пример.
3. Формулы дифференцирования степеной функции с любым действительным показателем, показательной функции, сложной показательной функции.
4. Формула дифференцирования сложной функции. Приведите примеры.
5.Теорема о производной обратной функции.
6. Формулы дифференцирования обратных тригонометрических функций.
7.Сформулируйте определение дифференциала функции. В чем заключается свойство инвариантности формы дифференциала функции?
8. На чем основано применение дифференциала в приближенных вычислениях?
Литература:
[2] Глава 4 § 4.1-4.8 стр. 127-150
[19] 3.1-3.2 стр. 180-188
[18] § 9.1-9.8 стр. 235-265
[20] § 9.1-9.8 стр. 157-187
Тема лекции: Прозводные и дифференциалы высших порядков. Основные теоремы дифференциального (2 часа)
8.1. Производные и дифференциалы высших порядков. Производная  называется еще первой производной функции
называется еще первой производной функции  или производной первого порядка, сама функция
или производной первого порядка, сама функция  называется производной нулевого порядка.
называется производной нулевого порядка.
Определение. Производной  – го порядка функции называется производная от её производной (
– го порядка функции называется производная от её производной ( -1) порядка при условии, что эти производные существуют
-1) порядка при условии, что эти производные существуют
 ,
,  = 1,2,3,…
= 1,2,3,…
функция f при этом называется  раз дифференцируемой..
раз дифференцируемой..
Пример. Дано  .
.
Первая производная 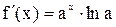 ,
,
вторая производная  ,
,
третья производная  .
.
Следовательно,
 ,
,  .
.
Эта функция бесконечно дифференцируема для 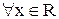 , т.е. она имеет производные всех порядков. Для суммы и произведения
, т.е. она имеет производные всех порядков. Для суммы и произведения  –раз дифференцируемых функций
–раз дифференцируемых функций  и
и 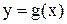 справедливы следующие правила дифференцирования (
справедливы следующие правила дифференцирования (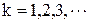 ):
):
1.  ,
,  .
.
2. Формула Лейбница:


 ;
;  .
.
Без доказательства.
Пример. Вычислить  по формуле Лейбница.
по формуле Лейбница.

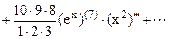 .
.
Заметим, что  и
и  , поэтому
, поэтому 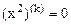 при
при  и последующие слагаемые также равны нулю, следовательно,
и последующие слагаемые также равны нулю, следовательно,
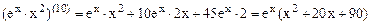 .
.
Пусть функция 
 –раз дифференцируема.
–раз дифференцируема.
Дата публикования: 2014-10-23; Прочитано: 985 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
