 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Параметрически заданная функция и её производная
|
|
Функцию  иногда удобно записывать в параметрическом виде
иногда удобно записывать в параметрическом виде
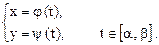
Таким образом описывается движение точки на плоскости в механике (t – время, x, y – координаты точки).
Пример. Функция, графиком которой является полуокружность радиуса 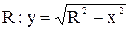 имеет параметрическую запись
имеет параметрическую запись
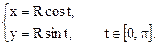
Если положить 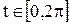 , то получаем всю окружность
, то получаем всю окружность 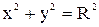 , которую нельзя задать с помощью графика одной функции.
, которую нельзя задать с помощью графика одной функции.
Теорема. Пусть функция 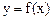 задана в параметрическом виде
задана в параметрическом виде
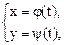
где j и y определены в окрестности 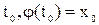 . Тогда, если производные
. Тогда, если производные 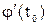 и
и 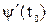 существуют и
существуют и 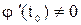 , то функция
, то функция  дифференцируема в точке
дифференцируема в точке 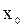 и
и
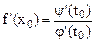 .
.
Пример. Кривая, являющаяся траекторией движения точки на ободе колеса радиуса а, катящегося по оси ОХ, называется циклоидой (рис 9). Её параметрические уравнения:
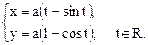
Эта кривая не является графиком никакой элементарной функции, поэтому производную от этой функции 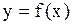 можно вычислить только в параметрическом виде
можно вычислить только в параметрическом виде
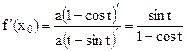 .
.
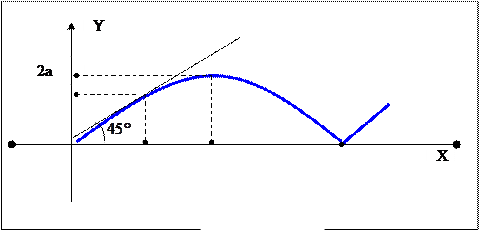
Рис. 9
Например, при 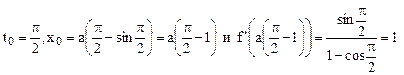 ,
,
т.е. угол наклона касательной к графику функции в этой точке равен 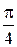 .
.
Дата публикования: 2014-10-23; Прочитано: 440 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
