Классификация точек разрыва

Определение. Точка , в которой нарушается хотя бы одно условие непрерывности функции 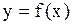, называется точкой разрыва этой функции.

Рассмотрим точку разрыва функции 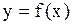, в некоторой окрестности которой (кроме быть может ) эта функция определена. Возможны три случая:

1. Если 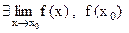не определена или , то называется точкой устранимого разрыва.

Если эту функцию изменить в точке , т. е. положить

то функция будет непрерывной в точке , т. е. этот разрыв устраняется.

Пример. Функция имеет устранимый разрыв в точке . Если положить

то функция будет всюду непрерывна (рис.11).

Рис.11

График функции

2. Если , то точка называется точкой разрыва первого рода функции .

Пример. Для функции

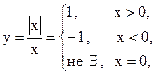
точка является разрывом первого рода (рис.12)

Рис.12

3. Если хотя бы один из пределов не существует или равен бесконечности, то точка называется точкойразрыва второго рода функции .

Пример. Для функции , точка является разрывом второго рода, так как

(не существует) (рис.13).

Рис.13