Непрерывность функции. Определение. Функция называется непрерывной в точке , если выполняются три условия:

Определение. Функция называется непрерывной в точке , если выполняются три условия:

1) существует ;

2) существует ;

3) .

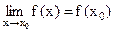В символической форме это определение записывается так:

.

Функция называется непрерывной в точке слева (справа), если выполняются три условия:

1) ;

2) .

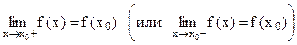Очевидно, что функция является непрерывной в точке в том и только в том случае, когда она непрерывна в этой точке слева и справа.

График непрерывной функции представляет из себя непрерывную линию.

Теорема (о непрерывности монотонной функции). Пусть функция монотонна (монотонно возрастает или монотонно убывает) на отрезке [а, ] и принимает все значения из отрезка , тогда она непрерывна в каждой точке интервала (а, ), непрерывна в точке а справа и в точке слева. (рис.9)

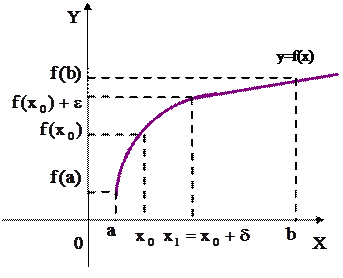Рис. 9

Из этой теоремы следует, что все основные элементарные функции непрерывны во всех внутренних точках своей области определения, а во всех граничных точках области определения, принадлежащих ей, они непрерывны справа и слева. Это следует из того, что любую точку из области определения основной элементарной функции можно включить в отрезок, где эта функция монотонна и принимает все значения из отрезка .

Например, функция непрерывна во всех точках интервала

(–1,1), непрерывна в точке справа и в точке 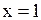слева, так как оно монотонно возрастает в и для

.

Теорема Пусть функци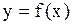и и непрерывны в точке . Тогда функции

1) , 2) , 3) при .

также непрерывны в точке .

Теорема (непрерывность сложной функции). Пусть функция 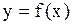непрерывна в точке и , а функция непрерывна в точке . Тогда сложная функция непрерывна в точке .

Рис. 10

Следствие 1. Если и функция непрерывна в точке , то .

Пример. .

Следствие 2. Любая элементарная функция непрерывна во всех внутренних точках своей области определения, а в граничных точках отрезков области определения непрерывна справа или слева.

Это следует из теорем 1, 2, 3.