Завдання 4. Розв’язати задачу Коші

,

Розв’язання. Дане рівняння – лінійне рівняння першого порядку. Розв’яжемо відповідне лінійне однорідне рівняння

.

Перепишемо це рівняння з відокремлюваними змінними у вигляді:

.

Поділивши змінні, дістанемо

, , ,

, ,

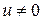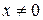де 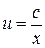-загальний розв'язок вихідного однорідного рівняння.

Знайдемо розв'язок вихідного неоднорідного рівняння методом варіації довільної сталої [1, с.281].

, де - невідома функція.

Підставимо у вихідне рівняння і .

Маємо .

Звідси .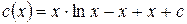

Загальним розв'язком лінійного неоднорідного рівняння є

.

Враховуючи початкові умови, здобудемо , звідси .

Отже, розв'язок задачі Коші має вигляд .

Завдання 5. Знайти загальний розв’язок рівняння:

Розв’язання. Перепишемо дане рівняння у вигляді

.

За ознакою це – рівняння Бернуллі [1, с.33]. Розв’яжемо його методом Бернуллі-Фур’є.

Нехай , тоді .

Тоді дане рівняння набуває вигляду

, або .

Функцію виберемо так, щоб

Маємо ; ; ;

,

тоді ,

, , ,

, .

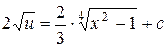Тепер маємо .

Завдання 6. Знайти загальний розв’язок рівняння:

.