 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Зі сталими коефіцієнтами
|
|
Лінійним однорідним диференціальним рівнянням 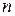 -го порядку зі сталими коефіцієнтами називається рівняння
-го порядку зі сталими коефіцієнтами називається рівняння
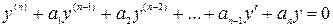 ,
,  (1)
(1)
у якому функція та ії похідні мають перший степінь, та коефіцієнти  - сталі.
- сталі.
Загальний розв’язок лінійного однорідного рівняння (1) має вигляд
 , (2)
, (2)
де  - лінійно незалежні на
- лінійно незалежні на  частинні розв'язки (фундаментальна система розв’язків) цього рівняння, а
частинні розв'язки (фундаментальна система розв’язків) цього рівняння, а  - довільні сталі.
- довільні сталі.
Лінійно незалежні частинні розв’язки рівняння (1) необхідно шукати у вигляді  . Це зводить рівняння (1) до алгебраїчного рівняння ступеню
. Це зводить рівняння (1) до алгебраїчного рівняння ступеню 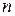
 , (3)
, (3)
яке називають характеристичним.
Далі необхідно знайти усі корені рівняння (3). Лінійно незалежні частинні розв’язки рівняння (1) будуються залежно від характеру коренів рівняння (3) згідно наступним правилам:
1) кожному дійсному однократному кореню  характеристичного рівняння відповідає частинний розв’язок
характеристичного рівняння відповідає частинний розв’язок  рівняння (1);
рівняння (1);
2) кожній парі однократних комплексно-спряжених коренів  і
і  відповідають два частинних лінійно незалежних розв’язка рівняння (1):
відповідають два частинних лінійно незалежних розв’язка рівняння (1):  і
і  ;
;
3) кожному дійсному кореню  кратності
кратності 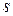 відповідає
відповідає 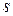 лінійно незалежних частинних розв’язків рівняння (1)
лінійно незалежних частинних розв’язків рівняння (1)  ;
;
4) кожній парі комплексно-спряжених коренів  і
і  кратності
кратності 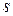 відповідають
відповідають  частинних лінійно незалежних розв’язків рівняння (1):
частинних лінійно незалежних розв’язків рівняння (1):
 ;
; 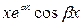 ;
;  ;...;
;...; 
 ;
;  ;
;  ;...;
;...;  .
.
Дата публикования: 2014-10-20; Прочитано: 503 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
