Зразок виконання розрахунково-графічної роботи №4

за темою " Д иференціальні рівняння "

Завдання 1. Знайти загальний розв’язок рівняння:

.

Розв'язання. Подамо дане рівняння з відокремлюваними змінними у вигляді:

.

Помноживши обидві частини рівняння на і розділивши на , маємо

або .

Інтегруючи, знаходимо

або

Відповідь: загальний розв'язок .

Завдання 2. Знайти загальний розв’язок рівняння:

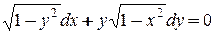
Розв'язання. Це рівняння з відокремлюваними змінними. Перепишемо його у вигляді .

Розділивши обидві частини рівняння на , маємо

.

Інтегруючи, дістанемо

або ,

- загальний розв'язок.

Якщо , , або .

Безпосередньою підстановкою перевіряємо, що:

та - розв'язки рівняння.

Завдання 3. Знайти загальний розв’язок рівняння:

.

Розв'язання. Це рівняння з однорідною функцією. Перепишемо його у вигляді .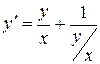

Замінимо , де , тоді та .

Підставимо це в дане рівняння

, або .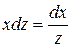

Розв’яжемо здобуте рівняння з відокремлюваними змінними

, , або , .

Повертаючись до невідомої функції , дістаємо, що .

Відповідь: .