Інтегруючий множинник

Якщо ліва частина рівняння

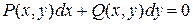
є повний диференціал деякої функції двох змінних , то таке рівняння називається рівнянням у повних диференціалах. В цьому випадку його можна переписати у вигляді . Тоді його загальний інтеграл дорівнює

(1)

Для того, щоб рівняння було рівнянням у повних диференціалах, необхідно і достатньо, щоб в усіх точках області D, в якій функції і визначені, неперервні і мають неперервні частинні похідні і , здійснювалась умова

= (2)

У тому випадку, коли умова (2) виконана, загальний інтеграл рівняння можна записати у вигляді

або

де – довільна фіксована точка області D.

Якщо ж умова не виконана, то рівняння не є рівнянням у повних диференціалах. Проте в деяких випадках його можна привести до рівняння у повних диференціалах множенням на функцію, яка називається інтегруючим множинником.

Інтегруючий множинник легко знаходиться в наступних двох випадках:

1. коли він залежить тільки від x, тобто ,

2. коли він залежить тільки від у, тобто .

Перший з цих випадків має місце, якщо відношення

є функцією тільки від x; тоді інтегруючий множинник знаходиться за формулою .

Другий випадок має місце, якщо відношення

є функцією тільки| від у; тоді інтегруючий множинник визначається за формулою .

2.1.6. Диференціальні рівняння вищих порядків, |